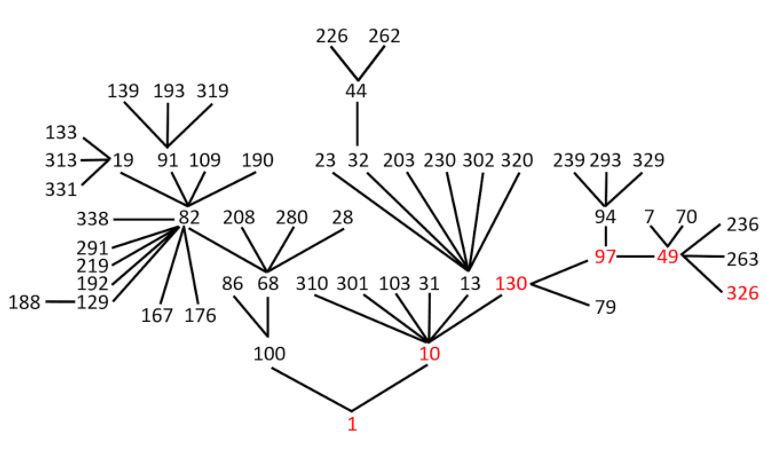
Continuing my search for biomedical black swans, based on the words newly cited in the Oxford English Dictionary (OED) from 1970 to 2020, I now turn to terms relevant to microbiology and infectious diseases. Of 90 terms I’ve surveyed, 52% describe viruses and viral diseases and 18% bacteria and bacterial diseases. The names of the bacteria are derived about equally from Latin and Greek words, whereas about one third of the names of the viruses are purely Latin in origin, and about one quarter are abbreviations; seven have combined Latin and Greek origins and seven are toponyms (Table 1).

Table 1. Toponymic viruses, named since 1970

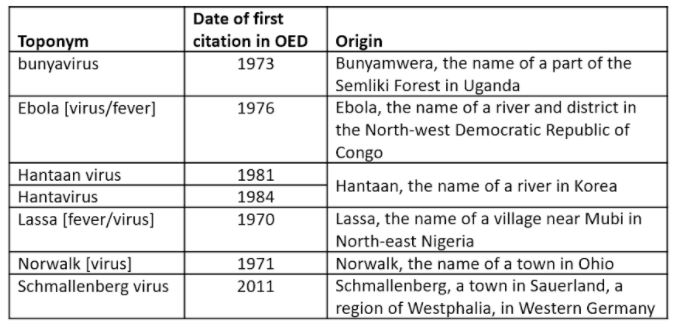
Toponymic nomenclature of infections and infectious organisms has been criticized recently, because of pejorative or accusatory uses, as if the rise of the infection was the fault of those who live in the area after which the causative organism was named. Toponymic infections include Bornholm disease and Marburg disease, but the best known is the Spanish flu, the 1918–20 influenza pandemic. It was so called, not because it was first observed in Spain, which is the usual toponymic justification, but because, in the absence of war-time press censorship, the Spanish newspapers provided extensive coverage of the pandemic. 

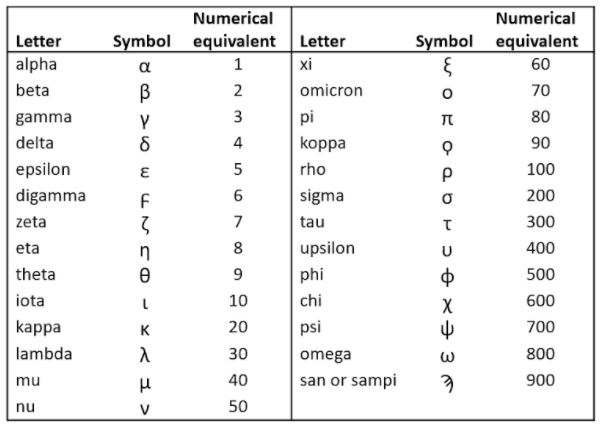
Now the variant of SARS-CoV2 previously called the Indian variant, also known less memorably as B.1.617.2, is to be called the delta variant, to avoid any implication that India was responsible for it. The Greek alphabet has 24 characters, from alpha to omega, but there are three others, present in early scripts but obsolete in Attic times, known collectively as episema (singular episemon)—a word that surprisingly has not made it into the OED. The letters were called digamma, koppa, and san or sampi, and they were retained in Attic Greek to symbolize numerals, since 27 letters are needed to cover all the integers from 1 to 999 (Table 2).

Table 2. The 27 letters of the Greek alphabet used to represent numerals

The digamma, which sounded like a vee or ef, can be seen in some Latin words that came from Greek before the digamma was dropped. Take the Attic Greek word for a ship, ναῦς (naus), from which we get nautical; in Latin it was navis, which gives us navigate. The Greek word for a key was κλείς (kleis), from which we get the musical instrument the ophicleide; in Latin it was clavis, which gives us a different instrument, the clavichord. In Greek, wine was οἶνος (oinos), but in Latin vinum, giving us wine, vine, vinegar, viniculture, vintage, and vinyl—the radical isomeric with ethenyl. In all these cases Latin retained the digamma, converting it to a vee.

The episema are unlikely to be harnessed to designate the 25th to 27th variants of SARS-CoV2, when they emerge. Perhaps Oxford’s way of grading students’ work will prove useful, with marks such as alpha, beta-plus, and, for finer distinctions, alpha-beta-double-plus-minus.

So what about the microbiological black swans? The antibiotic action of penicillin undoubtedly qualifies. But its isolation from a Penicillium mould by Florey. Chain, and Heatley was a planned effort, and thereafter antibacterial drugs were specifically sought, starting with the Actinomycetes, soil organisms in which Selman Waksman discovered streptomycin and from which many other antibacterial agents were later isolated.

The death on 16 April of the pharmacologist Ronnie Cresswell also reminds us of the discovery of azidothymidine (AZT), later called zidovudine, the first effective specific treatment for HIV AIDS. It had been synthesized in 1964 by Jerome Horwitz at the Michigan Cancer Foundation, who had hoped to use it as an antimetabolite in leukaemia. It didn’t prove useful, but in 1974 Wolfram Ostertag in the Max Planck Institute in Göttingen showed that it inhibited replication of a leukaemia retrovirus. So when Cresswell, leading drug development at Burroughs Wellcome, wanted to find a drug to inhibit the growth of HIV in vitro, his colleagues screened a range of compounds against other retroviruses, and there was AZT. A nucleoside chemist at Wellcome, Jane Rideout, chose it as one of a range of 14 different compounds, and her virologist colleague, Martha St Clair, did the screening. If that was a black swan, it took a long time to come out of hiding. Perhaps we can regard it as dark grey.

Infections are not black swans, in the sense of discoveries that are made unexpectedly. Rather they discover us, as it were, not we them. It is as if the black swan has suddenly decided to show itself. Perhaps we should call them ugly ducklings.

Jeffrey Aronson is a clinical pharmacologist, working in the Centre for Evidence Based Medicine in Oxford’s Nuffield Department of Primary Care Health Sciences. He is also president emeritus of the British Pharmacological Society.

Competing interests: none declared.

This week’s interesting integer: 326 Foyle’s triangle Write down all the integers one after the other starting with 1 on its own, followed by 2 and 3 in the row below it, then 4, 5, and 6 in the next row, and so on; the first 26 such rows are shown below; the 26th starts with 326: The numbers on the left-hand side of the triangle (numbers in blue) are the so-called pancake numbers (also called lazy caterer’s numbers and central polygonal numbers): ○ 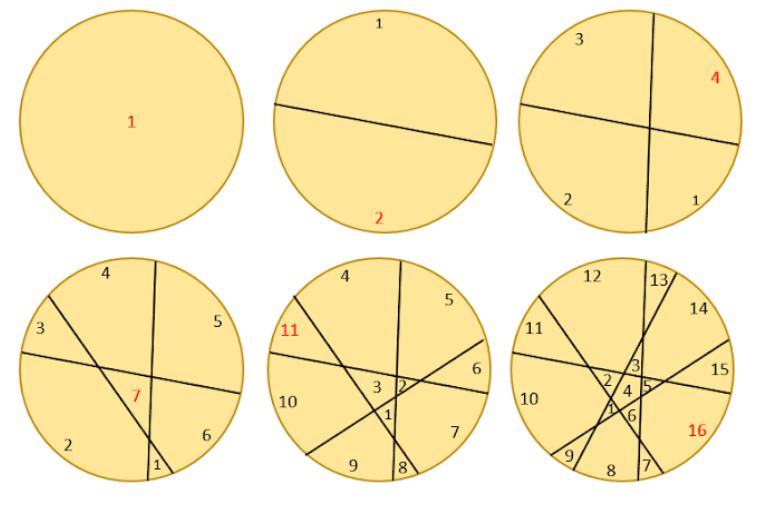Slice a pancake once and you get two pieces; add a slice and you get four pieces; add a third slice and you get, not eight, but seven pieces; four slices give you 11 pieces, five give you 16 (see the pictures below) and so on; if you slice 25 times you get 326 pieces The numbers on the right-hand side of Foyle’s triangle (the numbers in green) are the triangular numbers The circled triangular numbers are doubly triangular: the first triangular numbers are 1, 3, 6, 10, 15, and 21; the 3rd triangular number (T3) is 6; T6 is 21; T10 is 55; T15 is 120; T21 is 231; and so on; these are the doubly triangular numbers The numbers in black on the far right of Foyle’s triangle are the sums of the numbers in the corresponding rows; these numbers are the constants of the magic squares that contain the integers from 1 to n2, where n is the number of the row; for example, 15 is the sum in row 3 and it is the constant of a 3 × 3 magic square containing the integers 1 to 9; 34 (row 4) is the constant of a 4 × 4 magic square containing the integers 1 to 16; 65 (row 5) is the constant of a 5 × 5 magic square containing the integers 1 to 25; and so on: Toothpicks We have seen different types of toothpick patterns before (here, here, and here); 326 features in the toothpick pattern called leftist toothpicks. Starting with a single toothpick, add toothpicks at free ends, but when the toothpick is horizontal use only the left end; the first four steps are shown in (a), (b), (c), and (d) below: After 25 iterations you get 94 toothpicks:   55 iterations would give you 326 toothpicks Palindromes 326 + 623 = 949, a palindrome 326 is palindromic in both base 12 (232) and base 13 (1c1); it is the smallest number with that property Primes and semiprimes 326 is a semiprime, being the product of two primes, 2 × 163; it is the 104th semiprime, S104 It is also an emirpimes, since its reverse, 623 is a semiprime = 7 × 89 326 = the 57th prime (P57) + 57 = 269 + 57 326 is the sum of all the digits in the first 38 primes, from 2 to 163 The sum of the first 326 primes is 325019, which is a prime 326 is the sum of the first 14 odd primes 3262 = 106276, which is the sum of two consecutive primes = 53129 + 53147 33 + 22 + 66 = 46687, which is a prime 326 = 2 × 163; 22 + 1632 = 26573, which is a prime There are 326 fours in all the four-digit primes 1/3 + 1/2 + 1/6 = 1; thus, the harmonic mean of the three digits is 3, which is a prime Named numbers 326 is a happy number: add 32 + 22 + 62 = 49; now add 42 + 92 = 97; repeat; since you eventually reach one, 326 is a happy number; see Interesting integer 262 and the diagram below, which shows all the happy numbers up to 338, with 326 highlighted: 326 is an untouchable number, an integer that cannot be expressed as the sum of all the proper divisors of any other number Sums of 326 326 is the sum of three squares in six different ways: 12 + 12 + 182; 12 + 62 + 172; 12 + 102 + 152 ; 32 + 112 + 142; 62 + 112 + 132; and 72 + 92 + 142 It is the sum of eight distinct squares = 12 + 22 + 32 + 52 + 62 + 72 + 92 + 112 It is the sum of two triangular numbers in two different ways: ○ T1 + T25 = 1 + 325 ○ T16 + T19 = 136 + 190 It is the sum of four consecutive numbers: ○ 80 + 81 + 82 + 83 It is the sum of 14 consecutive primes: ○ 3 + 5 + 7 + 11 + 13 + 17 + 19 + 23 + 29 + 31 + 37 + 41 + 43 + 47 It is the sum of five consecutive composite numbers in two different ways: ○ 63 + 64 + 65 + 66 + 68 Pythagoras There is one Pythagorean triples that includes 326 as a leg: 326, 26568, 26570; it is a multiple of 163, 13284, 13285 Fibonacci Start with 0, 0, 1; add the three numbers = 1; append it to the sequence and add the last three numbers = 2; continue; these numbers are called tribonacci numbers: 0, 0, 1, 1, 2, 4, 7, 13, 24, 44, 81, 149, … 326 is the sum of the first 12 tribonacci numbers