Comprehensive though the list of phobias in the Oxford English Dictionary (OED) is, it omits some, notably gelotophobia. Nor does it include gelotophilia, katagelasticism, or gelasmus.
The IndoEuropean root KLEG meant to cry out or make a sound, an onomatopoeic form. In Greek κλαγγή (pronounced klangē) meant any sharp noise, such as the twang of a bow or the scream of a bird, specifically a crane. The future of the corresponding verb, κλάζω, was κλάγξω (klanxō), I shall scream, from which the makers of an early car horn derived a brand name, Klaxon.
In Latin the verb became clangere, from which we get clang and clangor, clack, click, and cluck, clank, clink, and clunk. Clinkum-clankum, later shortened to clink-clank, being a reduplicated form, signified a succession of clinking sounds and hence a senseless jingle.
To clink means to make a metallic sound, like the sound a clock might make when its hammer strikes a bell. A clinch or clench was a nail or bolt that would make such a sound when struck with a hammer. A clincher or clinker clinched the bolts in ship-building by bending them back or flattening the points. A clinchpoop may have been one who did that on the poops of vessels, and it then came to mean a rough worker or a boor, just as a clown was originally a peasant, giving us a putative link to laughter, which also comes from KLEG.
Latin clangere led to various Northern European forms, such as hlahtar (Old High German), hlakkia (Old Frisian), hlaeja (Old Norse), and hlaehhan (Old English), all meaning to laugh. The Old Irish word cluiche meant a joke. In German gelächter means laughter.
KLEG is an extended form of the IndoEuropean root KEL, to shout or resound, giving the Greek word for laughter, γέλως. Γελωτοφυλλις was the Greek name for Cannabis sativa, presumably because it was a plant (φυλλις) that excited laughter.
The Oxford English Dictionary (OED) lists only a few English derivatives of γέλως and related words. A gelasin is a dimple in the cheeks produced by smiling. Geloscopy, according to Nathaniel Bailey’s Dictionarium Britannicum (1730), is “a sort of Divination performed by means of Laughter; or a divining any Persons, Qualities or Character, by observation of the manner of his Laughing”. And a gelotometer is a gauge for measuring laughter. Gelastic means “serving the function of laughter, risible” and gelastics are remedies that act by eliciting laughter, perhaps with Humphry Davy’s laughing gas (nitrous oxide) in mind.
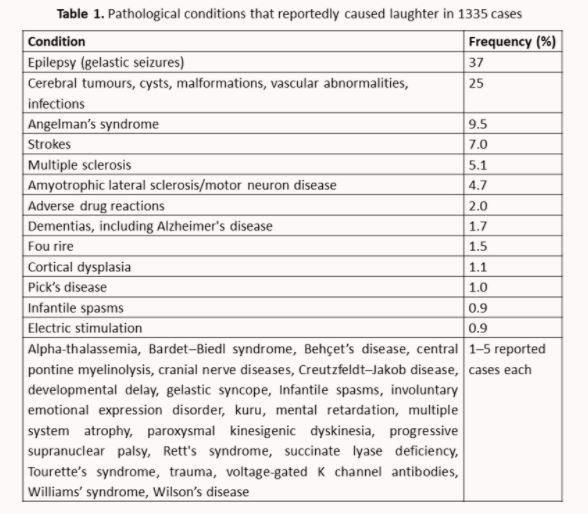
However, the OED does not refer to gelastic epilepsy, seizures that result in laughter, a term coined in 1957, nor to gelastic syncope, fainting caused by laughter. When Robin Ferner and I reviewed the benefits and harms of laughter in 2013, we found 1335 reports of pathological laughter; many were due to seizures (Table 1). Gelastic syncope is rarer.
There are other words, not found in the OED. Gelotophobia is fear of being laughed at. The earliest hit in PubMed is from 2010, but earlier instances can be found. For example, in 1996 the German psychoanalyst Michael Titze referred to the Pinocchio Complex as “a phenomenon that refers to those with gelotophobia, … people [who] have never learned to appreciate humor and laughter positively.” He suggested treatments. Gelotophilia, joy at being laughed at, is a later coinage, as is katagelasticism, joy in laughing at others (Greek κατάγελως, derision or a laughing-stock). And older than any of these is gelasmus, spasmodic laughter; it was listed in the Encyclopedia of Aberrations, which was edited by Edward Podolsky in 1953 and described by one reviewer as “an aberration in encyclopedias”.
The Greek word γελωτοποιός meant, and still means, a maker of laughter, a buffoon. Gelotopoietic should mean stimulating laughter, but I haven’t found it anywhere. Time to introduce it to describe the quality of stand-up comedians.
Finally, back to click-clacking. In French claque means a clap of the hands, and in English an organized body of applauders in a theatre. The claque in the Milan opera house La Scala, the loggionisti, who occupy the gods, the loggione, can make or break an opera singer. Ronald Reagan once told a story about Leoncavallo’s opera I Pagliacci (“Clowns”). A tenor, newly recruited to the company, performed the famous aria “Vesti la giubba” (“On with the motley”). The claque demanded encore after encore: “You’ll do it until you get it right.”
Jeffrey Aronson is a clinical pharmacologist, working in the Centre for Evidence Based Medicine in Oxford’s Nuffield Department of Primary Care Health Sciences. He is also president emeritus of the British Pharmacological Society.
Competing interests: None declared.
|
This week’s interesting integer: 288 • ABA numbers • Achilles numbers • Cunningham numbers • Jordan-Polya numbers and superfactorials • Pythagorean triples • Smooth numbers • Square manipulations: • 288 is the sum of: • 285 is a Harshad number (see Interesting integer 280), since it is divisible by the sum of its digits (18). • 288 is divisible by each of its digits; such numbers are called nude numbers. • 288 is a refactorable number (or a tau number), i.e. one that is divisible by its number of divisors. Here’s how you calculate the number of divisors of a number, including the number itself. First express it as the product of all its prime factors: 288 = 25 × 32. Now add one to each of the indices of the prime factors (in this case 5 and 2) and multiply them: 6 × 3 = 18. So 288 has 18 divisors. And 18 divides 288 exactly (288/18 = 16). • 288 is a self-number. Many numbers can be generated from other numbers in the following way: add the generating number to the sum of its digits. For example, in base 10, 265 can be generated from 254, since 265 = 254 + 2 + 5 + 4. However, there is no number that generates 288 in this way; in this sense it is by itself. Self-numbers are also called Colombian numbers and Devlali numbers. • Like 262, 268, and 276, 288 is an untouchable number, an integer that cannot be expressed as the sum of all the proper divisors of any other number. For example, the proper divisors of 9 are 1 and 3, whose sum is 4; therefore 4 is a touchable number, since it is the sum of the proper divisors of 9. There is no integer whose proper divisors add up to 288. Untouchable numbers are also called non-aliquot numbers. • 288 is the ninth pentagonal pyramidal number, having the form n2(n + 1)/2, where n = 8. • 288 is the 53rd entry in Aronson’s sequence. |
