Last week I suggested that there is widespread misunderstanding about the meaning of “exponential” in mathematics. Colloquially, it means a huge increase, which it need not be. And when events change exponentially they can go down as well as going up. Considering how you invest your money introduces the way in which exponentials work.

Suppose you invest £100 at a simple interest rate of 10 per cent per annum. Each year you earn £10. The principal, what you have in the bank that has conned you into this deal, increases linearly (Table 1). Now you strike a better deal; instead of a fixed percentage of your principal (£100) each year, the bank will give you a fixed percentage of the cumulative amount. Now you do somewhat better (Table 1). Instead of increasing your principal by 120% after 20 years (6% per annum) you increase it by 220%, an annual average of 11%.

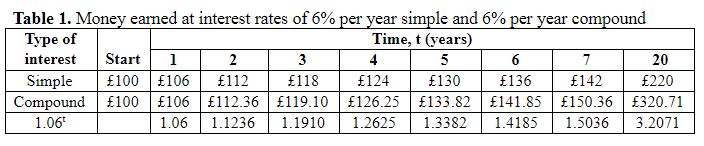
Let’s call the principal P and the rate of interest k. In the case of simple interest, the amount, A(t), you have in the bank at any time, t, is given by the following equation: A(t) = P + (kP × t). So, for example, when the rate of interest is 6% the amount you have after 5 years, A(5), can be calculated as A(5) = 100 + (0.06 × 100 × 5) = £130 (as in Table 1).

However, when compound interest is calculated on the cumulative amount, the equation becomes more complicated. In the first year the calculation is the same as for simple interest:

• Year 1: A(1) = P + kP. In this case that’s 100 + (0.06 × 100) = £106.

But in the second year P becomes the new amount P + kP and so the equation becomes:

• Year 2: A(2) = (P + kP) + k(P + kP). That’s 106 + (0.06 × 106) = £112.36.

And in the third year we have to use this new amount in the calculation:

• Year 3: A(3) = [(P + kP) + k(P + kP)] + k[(P + kP) + k(P + kP)] = £119.10.

We can keep on doing this and writing longer and longer equations. However, there is a simpler way of expressing it. If P increases by 6% each year it will grow at a rate of 1.06^t, as shown in Table 1. After 20 years you will have £320.71 in the bank (100 × 1.06²⁰). Before the days of electronic calculators you would have done this calculation using logarithms.

Now you negotiate a better deal with the bank. Why not get 3% every 6 months? Or 0.5% every month? Or even 6/365 = 0.000164% every day? What would you have after 20 years?

• Year 20: A(20) = 100 × 1.000164^{20 ×365} = £325.67.

You might be surprised that this new amount, calculated day by day, isn’t much more than it was when calculated year by year, with the same total interest. If you did it hour by hour the answer would be £332.01, not much more again.

What we did was to calculate P(1 + k)^t. Dividing k, the interest rate, by the number of days or hours or whatever, we calculated P(1 + k/n)^nt, where n is the number of days in a year (365) or the number of hours (8760). For example, 100(1 + 0.06/8760)^8760×20 = £332.01.

Thus, the basic growth rate is given by (1 + 1/n)ⁿ. When we increase n from one to very large numbers a surprising thing happens. The result doesn’t go on increasing, or not by very much (Table 2). It reaches a limit of about 2.71828. And that limit has been given a symbol, the letter e. Enter a 1 into your calculator and press the key marked e^x. You’ll get 2.71828….

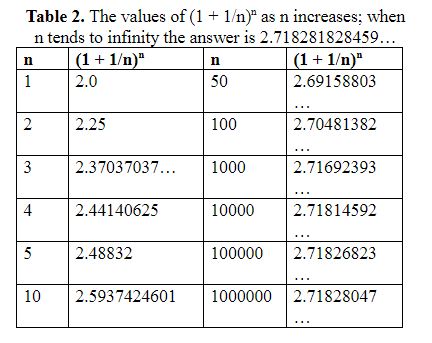
This number, which the Swiss mathematician Leonhard Euler called e, is the constant of natural growth. And instead of basing logarithms on 10^x, where x is the logarithm of 10^x, you can base it on e^x, where x is the logarithm of e^x, the natural logarithm (ln, as it is commonly called). So our principal increases by a factor of e^kt, the expression of exponential change.

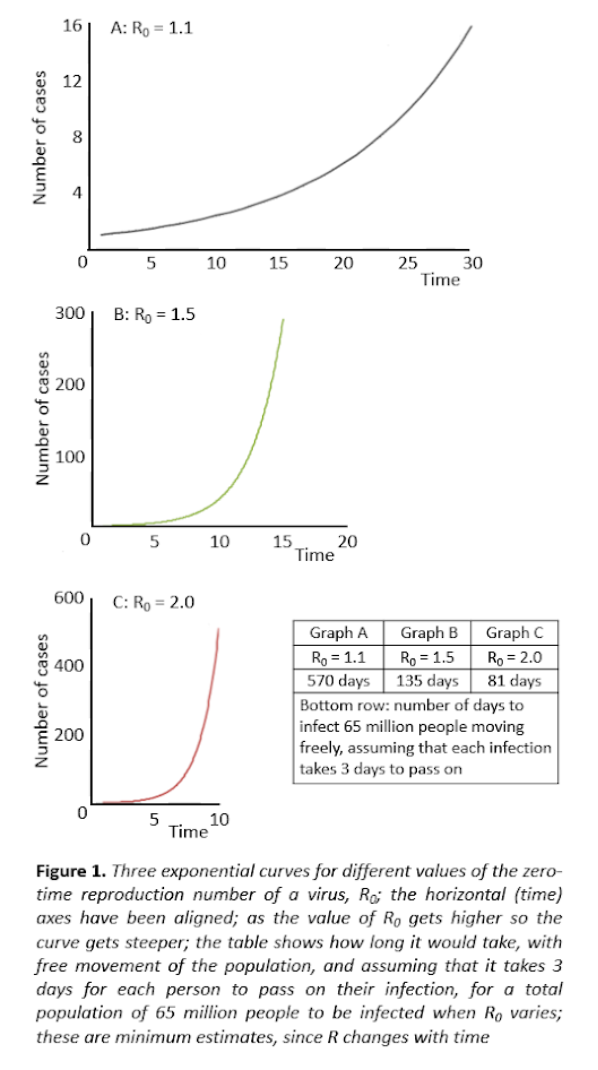
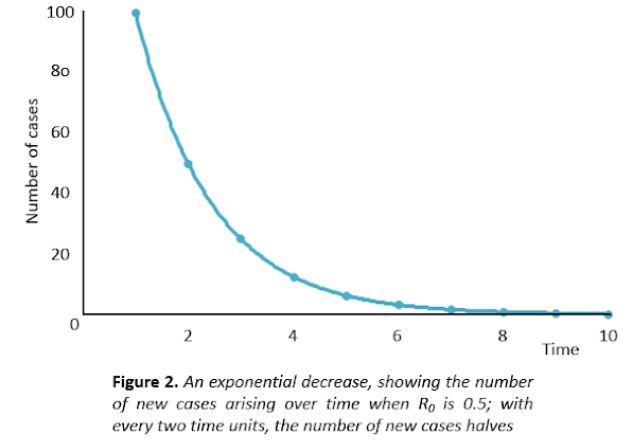
What has all this to do with R₀ and R_e the reproduction numbers of a virus? Well if R is 2, each person infects two people; so the first 100 people to be infected will infect 200 other people; those 200 infect another 400; those 400 infect 800. And so it goes, doubling all the while. That’s an exponential increase. Even if R is only just above 1, say 1.1, the number of people will increase exponentially, but not as fast as when it was 2 (Figure 1). Suppose R falls to less than 1 during an epidemic, say 0.5. Then the first 100 people will infect another 50; they will infect 25, and so on; that’s an exponential decrease (Figure 2) and the epidemic will die out.

Remember: the value of your investment can go down as well as up.

Jeffrey Aronson is a clinical pharmacologist, working in the Centre for Evidence Based Medicine in Oxford’s Nuffield Department of Primary Care Health Sciences. He is also president emeritus of the British Pharmacological Society.

Competing interests: None declared.