 In all the recent talk about tit for tat, whether in the spheres of diplomacy or trade, whose origins I discussed last week, there has been little if any discussion of whether it is a profitable strategy. A game theory analysis of a problem called the Prisoner’s Dilemma provides insights.
In all the recent talk about tit for tat, whether in the spheres of diplomacy or trade, whose origins I discussed last week, there has been little if any discussion of whether it is a profitable strategy. A game theory analysis of a problem called the Prisoner’s Dilemma provides insights.
Imagine that you and an accomplice have committed a crime and are being interrogated by the fuzz, the bluebottles, the slops, the rozzers. They tell you that they have enough evidence to prove you did it and to send you away, bang you up, for 2 years. However, if you spill the beans, fess up, and implicate your partner you will get away scot free and he will get 5 years. On the other hand, if he does likewise and you do not, the sentences will be reversed. And if you both confess you will both get 4 years. What do you do? If you trust your partner to keep shtoom, zip his lip, you will shop him, grass, snitch. And he is in the same position. But can you trust him? Can he trust you? Look at the payoff matrix (Figure 1). If you keep shtoom your average expectation is 3½ years in the clink (a half of 2 + 5). If you do the dirty, your average expectation is 2 years. So you decide to sell out. If your accomplice is equally logical he will do the same and you will both get 4 years. Of course, you would both have done better to keep shtoom, but you just can’t trust each other to do that. Defecting is the only sensible course.
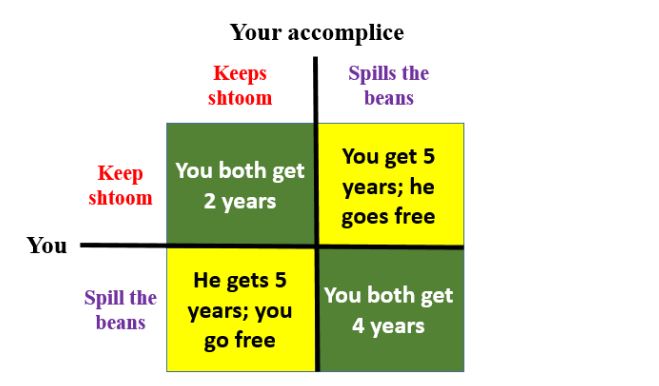
Figure 1. The payoff matrix for the Prisoner’s Dilemma
In the more general form of this problem two parties either want to cooperate in some endeavour or prefer to defect. Here’s the payoff matrix for this version (Figure 2).
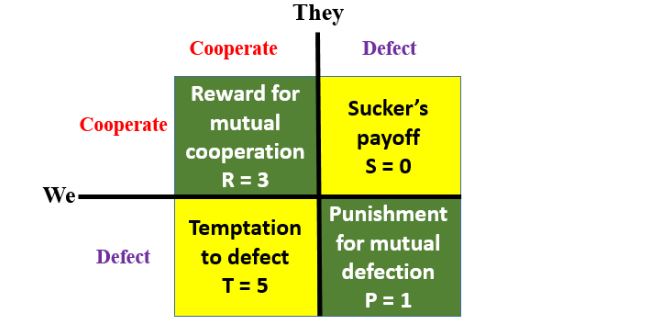
Figure 2. The payoff matrix for the general form of the Prisoner’s Dilemma; the payoffs are designed such that T>R>P>S and R > (S +T)/2
What happens if we play the game repeatedly? Is there a best long term strategy? In 1980 Robert Axelrod, professor of political science at the University of Michigan, invited a group of game theorists to design strategies that they thought would maximise their payoffs in repeated games. Fourteen programs were submitted and Axelrod played the programs off against each other in a computerised round robin tournament. The program called Tit for Tat won. Axelrod then invited the participants to revise their programs in the light of the results and invited others to join in. The author of Tit for Tit, Anatol Rapoport, left his program unchanged. Out of 62 entries, Tit for Tat won again.
The strategy adopted by Tit for Tat was simple: cooperate on the first round and then copy your opponent’s move on each successive round. If your opponents defected last time, you should defect; if they cooperated you should cooperate. Playing tit for tat paid off. It wasn’t the best possible program (for example, it could only play randomly against another random program), but its aggregate points were higher than any other program in the tournament.
However, there are problems with the conclusion that tit for tat is the best strategy in the iterative game. Firstly, others have failed to replicate this result, and tit for tat can be beaten, for example by a win-stay/lose-shift strategy. Secondly, tit for tit prevailed because it amassed more points than its opponents, while not actually winning any games. If this seems odd, remember that you can win an election in, say, America, even when you fail to win a majority of all the votes. And tit for tat’s success was determined by the method of scoring that Axelrod used; had he chosen different designs, other programs would have won. In other words, we really don’t know what the best strategy is for winning the iterative Prisoner’s Dilemma.
The idea of deliberate tit for tat has at times been misunderstood. For example, medical students doing a clerkship in emergency medicine were required to evaluate a resident or faculty before they were allowed to see their assessments; this increased the number of evaluations from a mean of 3.60 to 8.19 evaluations per student. The authors described this as a tit for tat strategy, but it wasn’t, just an inducement. In a case of status epilepticus that caused increased autonomic nervous system activity, neurogenic cardiomyopathy with left ventricular hypokinesia resulted and in turn caused an embolic stroke. The authors called this “tit for tat”, as if the heart was somehow deliberately hitting back at the brain for damaging it; fortunately, the brain seemed not to know about tit for tat, or the mutual damage might have escalated.
This is perforce too simple an account of the complexities of the iterative version of the Prisoner’s Dilemma, but I hope that it may have whetted appetites for reading more. However, be warned: the tit for tat strategy has been widely discussed and one of Axelrod’s papers, co-written with the evolutionary biologist William Hamilton, has been cited over 35 000 times.
Jeffrey Aronson is a clinical pharmacologist, working in the Centre for Evidence Based Medicine in Oxford’s Nuffield Department of Primary Care Health Sciences. He is also president emeritus of the British Pharmacological Society.
Competing interests: None declared.
