Last week I outlined some basic pharmacokinetic principles that can inform the likelihood that a newly proposed treatment may be effective, given only in vitro evidence. I showed that the highest tissue concentrations of ivermectin that are likely to be achieved after a single standard dose, the usual mode of administration, or even during repeated use of high doses to steady state, would fall a long way short of the in vitro concentrations that are needed to inhibit the SARS-CoV-2 virus, making ivermectin an unlikely candidate for effective treatment. Pharmacodynamic analysis can also be useful in predicting potential efficacy.
“Pharmacodynamics”, like “pharmacokinetics”, comes from two Greek words, in this case ϕάρμᾰκον and δύνᾰμις, power or might (Figure 1). The earliest uses of the noun “pharmacodynamics” and the adjective “pharmacodynamic” in English are from 1836 and 1846 respectively, over 100 years before the appearance of “pharmacokinetics” in the late 1950s. “Pharmakodynamik” had already been used in German in 1823.
A pharmacodynamic effect involves an interaction between an extrinsic moiety, the drug, and an intrinsic moiety, which is usually a membrane-bound or intracellular receptor or an enzyme, or in the case of an infection some part of the infecting organism. Dexamethasone, for example, targets an intracellular host receptor; remdesivir targets the RNA-dependent RNA polymerase of the SARS-CoV-2 virus.
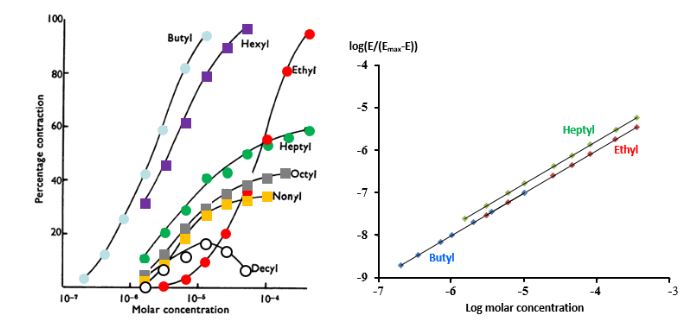
The law of mass action dictates that there will be a relation between the concentration of the drug and the effect that it has on its target. This is illustrated in Figure 2.
Figure 2. Concentration–effect relationships for a series of alkylated trimethylammonium salts causing contraction in guinea-pig ileum in vitro
The principle of the dose-response curve, stated in its simplest terms, is that:
- no effect occurs in the absence of a drug;
- the intensity of the effect increases when increasing concentrations of the drug are introduced;
- there comes a point at which further increases in concentration produce no further appreciable increase in effect, that effect being regarded as a maximum;
- in rare cases, increasing the concentration causes a reduction in the effect (hormesis)
The graph on the left (redrawn from Stephenson 1956) shows the concentrations used on a logarithmic scale, with the effects expressed as a percentage of the maximum possible effect, illustrating different potencies, different maximum efficacies, and in one case, the decyl salt, apparent hormesis, but probably an artefact; the graph on the right shows a different method of plotting the data, which linearizes three of the sigmoid curves shown on the left
It is possible to pick a potential therapeutic target and study in vitro the effect of a drug that is supposedly active at that target. And dose-responsiveness is an important criterion for predicting in vivo efficacy. However, even when dose-responsiveness is shown, there is no guarantee that the action will be translated into clinical efficacy, particularly if the concentrations required for in vitro effectiveness are higher than can be expected in vivo. Furthermore, the milieu of cells exposed to any drug in vitro will be unlike that of cells in vivo, with differences, for example, in oxygen tension, pH, and cation concentrations. Even when dose-responsiveness has been shown in vitro, expectations of viral inhibition have not translated into clinical efficacy in many cases. Take ivermectin, for example; it reportedly has antiviral activity in vitro against dengue fever virus, influenza virus, West Nile virus, and Venezuelan equine encephalitis virus, without good evidence of clinical efficacy.
Ivermectin has been suggested to have as its target a host protein known as importin α/β, which, as its name suggests, imports materials from the cytoplasm into the nucleus. SARS-CoV-2 proteins are synthesized and assembled in the cytoplasm, and although most remain there, some, such as its ribonucleoprotein, are imported into the nucleus for synthesis and genomic regulation and exported from it. However, the IC50 for binding of ivermectin to importin α/β is 17 micromol/L. Thus, on both pharmacokinetic and pharmacodynamic grounds, ivermectin is unlikely to have any therapeutic effect via an action on importins.
Of course, mechanistic reasoning of this sort generates a hypothesis, which even if encouraging needs testing in well designed clinical trials in large numbers of individuals. So what about clinical studies of ivermectin? I know of one retracted study, which has not been archived, one retrospective study, and one open pilot study in 16 patients with historical controls (a so-called “synthetic controlled arm”). We still await the results of well designed studies in large enough numbers of subjects with covid-19 to justify positive conclusions.
Our progress so far in finding a treatment for covid-19 accords with a dictum of Sir Robert Alexander Watson-Watt (1892–1973), the inventor of radar (picture): “Give them the third best to go on with; the second best comes too late, the best never comes.” This is known as the “cult of the imperfect”. We have so far been rewarded with a third best treatment in the form of remdesivir and a second best treatment in the form of dexamethasone.
Which leaves me to ponder the fact that the earliest uses of the noun “pharmacodynamics” and the adjective “pharmacodynamics” in English are to be found in the homoeopathic literature (Figure 3).
Figure 3. The earliest known instance of the word “pharmacodynamics”, from A Practical View of Homoeopathy by Stephen Simpson (1836); the epigraph on the title page is from a pensée of Montaigne, in which he discusses Molière’s play Le bourgeois gentilhomme: “Molière n’est jamais sorti de la nature; ce n’est sa faute si le vrai n’est pas toujours vraisemblable”
Jeffrey Aronson is a clinical pharmacologist, working in the Centre for Evidence Based Medicine in Oxford’s Nuffield Department of Primary Care Health Sciences. He is also president emeritus of the British Pharmacological Society.
Competing interests: None declared.
|
This week’s interesting integer: 284 • 284 is |