Last week I introduced the basic and effective reproduction numbers, respectively R0 and Re, that are estimated in studying the way a viral epidemic spreads through the population.
The basic reproduction number is defined as the number of cases that are expected to occur on average in a homogeneous population as a result of infection by a single individual, when the population is susceptible at the start of an epidemic, before widespread immunity starts to develop and before any attempt has been made at immunization. So if one person develops the infection and passes it on to two others, the R0 is 2.
The effective reproduction number, Re, is the number of people in a population who can be infected by an individual at any specific time. It changes as people become immune or die.
If the average R0 in the population is greater than 1, the infection will spread exponentially. If R0 is less than 1, or if Re falls to less than 1 during the epidemic, the infection will spread only slowly, and will eventually die out.
R0 is estimated from data collected in the field and entered into mathematical models. The estimate depends on the model used and the data that inform it. A typical model is based on three factors: individual susceptibility to the infection, the rate at which infections actually occur, and the rate of removal of infection from the population, by either recovery or death.
Since advice about how to behave during an epidemic, such as when to enforce isolation and when to relax restrictions, depends in part on estimates of Re, it is important that the models used to calculate it should be robust. So how good are the mathematical models?
Here’s a strikingly good example—the accuracy with which exit polls have predicted the outcomes of general elections. The American statistician Warren Mitofsky introduced exit polls in the 1960s, in a Kentucky governorship election. The idea may have been based on the habit of interviewing movie preview audiences as they left the cinema. However, exit polls had taken place in the USA as early as the 1940s, although the earliest instance of the term recorded in the Oxford English Dictionary is from a June 1976 article in the New York Times.
How do exit polls work? Polling is based on taking a random sample of the population and assuming that they are representative of the whole population. In UK exit polls about 200 voters are randomly sampled as they leave each of 144 of the 40 000 or so polling stations around the country and are asked how they have just voted; they may be asked to cast their votes again in a sham procedure, perhaps making them more likely to report exactly how they have just voted at the ballot box. They are also asked how they voted last time. The data are then modelled according to known demographic characteristics and country-wide variations and scaled up to the whole voting population using complex statistical techniques.
The results of the 2019 UK general election are shown in Table 1. The exit poll came as close as one could to the actual outcome without suspecting sorcery; the data were of high quality and the expected variability was well modelled, under reasonable assumptions.
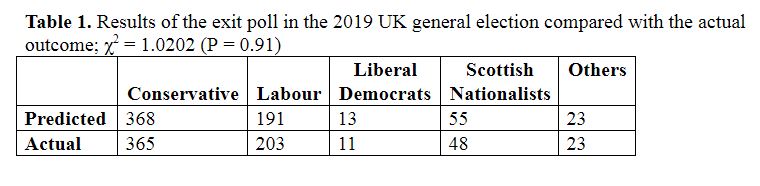
In contrast, modelling the spread of a virus is much more difficult, First, the data are incomplete; the number of infected individuals cannot be known accurately at any time because there are so many mild and asymptomatic cases; deaths cannot be completely counted and some deaths may be attributable to other causes, even in someone who has the infection. In addition, if other epidemiological knowledge, the equivalent of the well understood voting patterns and demographic effects in the exit poll models, is inadequate, modelling assumptions are likely to be inappropriate and inaccurate results are likely to emerge.
Thus, it has been exceedingly difficult to calculate accurately the reproduction numbers of SARS-CoV-2. Figure 1 illustrates this, with data taken from a systematic review of 21 studies, showing huge variation; the mean estimate was 3.32 (2.81–3.82) and the range 1.9–6.49.
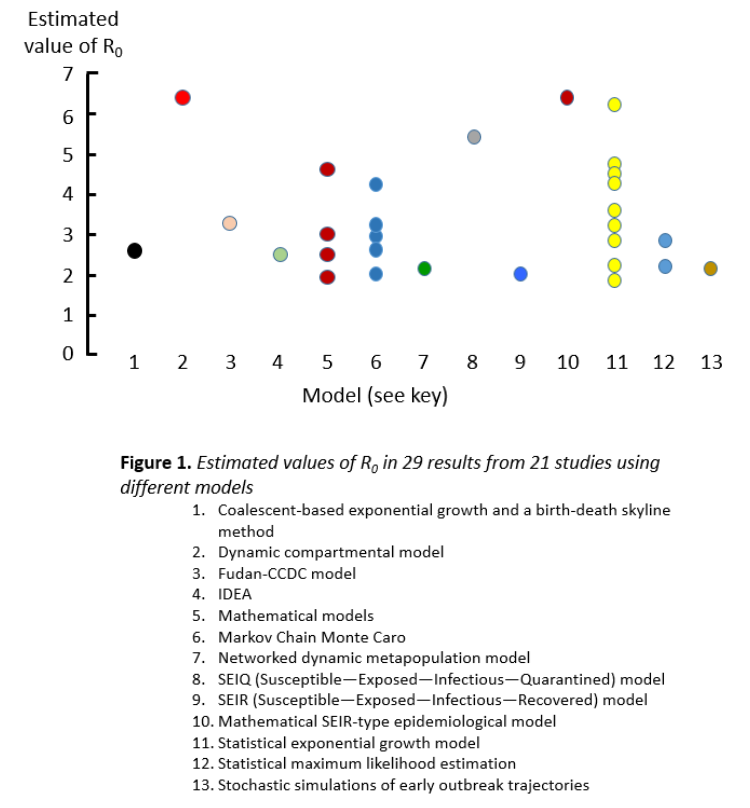
We should therefore recall George Box’s wise words about statistical models: “All models are wrong but some models are useful”. Or as he put it elsewhere, less dramatically but more specifically: “Models, of course, are never true, but fortunately it is only necessary that they be useful. For this it is usually needful only that they not be grossly wrong”. But the models being used to estimate the reproduction numbers of SARS-CoV-2 may be “grossly wrong”.
Jeffrey Aronson is a clinical pharmacologist, working in the Centre for Evidence Based Medicine in Oxford’s Nuffield Department of Primary Care Health Sciences. He is also president emeritus of the British Pharmacological Society.
Competing interests: None declared.
This week’s interesting integer: 269
162 + 32 + 22
Base 9 8 7 6 5 4 3 2 None of these numbers is a prime in base 10 except 269; for example 415 = 5 × 83. There is only one smaller number with this property, 263. |