As I wrote last week, a cellular automaton is a computational system with two components: an ordered array of cells and a set of rules that determines the state of each cell at any time, depending on its relation to other cells in its immediate locality.

A cell in such a system is generally represented by a square in the grid. The simplest state of such a cell is that it is either occupied (e.g. black) or unoccupied (e.g. white), on or off. An example of a simple rule is that a cell can be switched on if it is adjacent to a cell that it is already switched on. From such simple systems highly complex patterns can arise. Here’s an example.

Imagine a row of beds in a Nightingale-style ward, each represented by a cell in a one-dimensional array. A consultant visits one of his patients, represented by the black cell

Each time he comes to the ward thereafter he visits his other patients in an order that is determined by a simple rule: he will visit only those patients who have just one immediate neighbor who has already been visited. Anyone with no such neighbours or two such neighbours does not get visited. Here’s how the pattern of consultations builds up on successive visits:

Eventually all the patients get a visit, some lucky (or unlucky) ones more than once. In the following diagram each row represents a single visit to the ward, imagining the number of beds to be infinite:

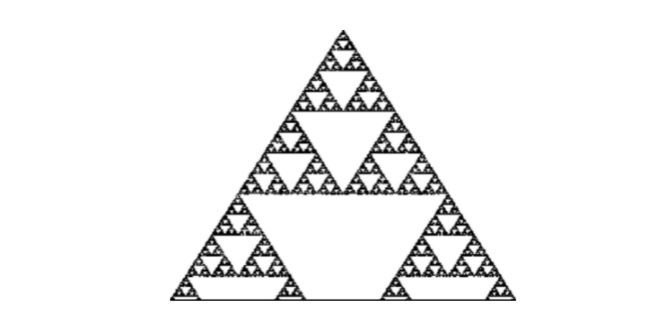
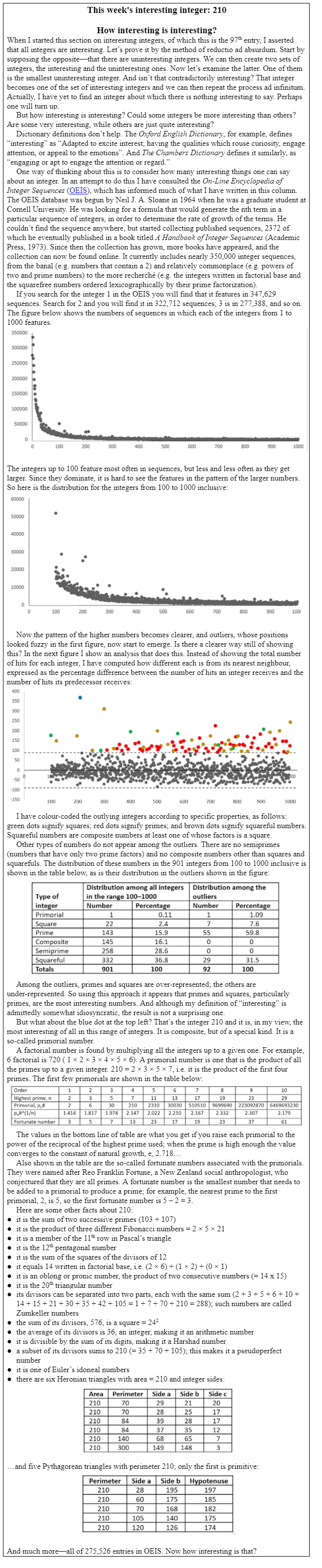
We have seen this pattern before; it is the Sierpiński triangle, a fractal pattern generated by recurrently removing inverted equilateral triangles from within larger upright equilateral triangles, or by shading in the odd numbers in Pascal’s triangle. The simplest of rules has generated an exceptionally complex pattern. And it is impossible to predict from any rule and any starting position what patterns will emerge.

Cellular automata are playing increasing roles in medical science. In illustration of this, Figure 1 shows the numbers of publications containing the term “cellular automat*” in a PubMed search up to 2020 (n =1596). With isolated exceptions from 1966 and 1981, papers started appearing in 1985 and have been steadily increasing in number ever since, particularly in the last few years. Recent papers have described, for example, studies of the effect of lockdown, migration, and vaccination on the dynamics of covid-19 and modelling its spread in Brazil.

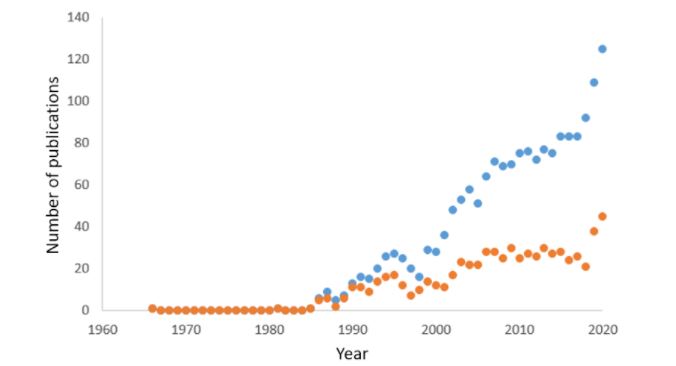
Figure 1. The numbers of publications year on year containing the term “cellular automat*”; blue: all publications; orange: titles (source PubMed)

Increasingly often our biological cells are being studied using computerized ones.

Jeffrey Aronson is a clinical pharmacologist, working in the Centre for Evidence Based Medicine in Oxford’s Nuffield Department of Primary Care Health Sciences. He is also president emeritus of the British Pharmacological Society.

Competing interests: none declared.