There are many types of fallacies and they are very common. The word comes from the Latin adjective fallax, deceitful or treacherous (of persons), misleading or deceptive (of things). The related verb is fallere, to trick or mislead, and the related noun is fallacia, deceptive behavior. In post-classical Latin fallacia came to mean a deceptive or misleading argument or a sophism, an instance of unsound or defective reasoning, and later an error or mistake. Specifically, in logic, it also came to mean an unintentional flaw of some sort that renders a syllogism invalid. When it is perpetrated deliberately, with the intention of deceiving, this is known as sophistry.
In medicine perhaps the most common fallacy is post hoc ergo propter hoc, literally “after that and therefore because of it”. This is the idea that because an outcome follows an intervention the latter must have caused the former. That this is not necessarily so is the basis of the scepticism with which anecdotal reports are generally treated. Occasionally, one may be able to demonstrate an association from one or a few cases, for example, between-the-eyes adverse drug reactions, but such associations are not common.
The only proper criterion among Bradford Hill’s much cited guidelines for causation is temporality. One cannot attribute association, let alone causation, if an outcome precedes an intervention. But even when the outcome follows the intervention, causation cannot necessarily be assumed; the relationship is not symmetrical.
However, it is equally fallacious to assume that when an association between an intervention and an outcome has been demonstrated, nothing need be done about it unless it can be shown to be causative. That is not the case. If, for example, an intervention brings little or no benefit but is associated with a serious adverse event, causation does not have to be proven before making a regulatory decision to withhold or restrict the intervention. Thalidomide was withdrawn from the market long before the association with fetal anomalies was shown to be causative.
Another type of fallacy that can affect medical practice arises from the phenomenon called the undistributed middle, explained in Box 1.
The politician’s fallacy is a variety of the fallacy of the undistributed middle: “Something must be done, this is something, therefore we must do it.” This version of the fallacy was first aired in an episode of the television programme “Yes Minister” in 1988, during a discussion between Sir Arnold and Sir Humphrey, two high-ranking civil servants. Sir Humphrey quotes the syllogism, and Sir Arnold replies that doing the wrong thing is worse than doing nothing. Sir Humphrey’s reply seals the deal: “Doing anything is worse than doing nothing”. This is the policy sometimes known as “masterly inactivity”, which I have previously called Fabian tactics, and which, in medical practice at least, is sometimes preferable to damaging intervention.
Inappropriate investigations and overdiagnosis may be on the increase. And inappropriate treatment, or therapeutic futility, may be hard to resist. But most things get better without intervention. Furthermore, masterly inactivity does not necessarily mean doing nothing. It may, for example, involve masterly surveillance of populations or monitoring of individuals, a watch and wait approach. Of course, the phrase “watchful waiting” appears to be oxymoronic: “watchful” implies activity and “waiting” implies passivity. But if surveillance and monitoring are in any sense watchful waiting, they combine both active and passive elements. Surveillance need not be qualified as either active or passive.
Sometimes the costs of inaction, both therapeutic and fiscal, outweigh the potential harms of intervening, and decisions can be hard to make. In all cases, however, the probable correct course can be assessed by contrasting the possible benefits of an intervention with its potential harms. To assume, as some sometimes do, that an intervention is bound to produce benefits, even when supported by the slimmest of evidence, without considering even the possibility of harms, is bad medicine.
Jeffrey Aronson is a clinical pharmacologist, working in the Centre for Evidence Based Medicine in Oxford’s Nuffield Department of Primary Care Health Sciences. He is also president emeritus of the British Pharmacological Society.
Competing interests: None declared.
|
This week’s interesting integer: 290
12 + 172; 32 + 52 + 162; 42 + 72 + 152; 52 + 112 + 122; 112 + 132.
T10 + T11 + T12 + T13 = 55 + 66 + 78 + 91 = 290.
5 + 6 + 7 + 8 + 9 + 10 + 11 + 12 + 13 + 14 + 15 + 16 + 17 + 18 + 19 + 20 + 21 + 22 + 23 + 24 56 + 57 + 58 + 59 + 60 71 + 72 + 73 + 74
67 + 71 + 73 + 79 56 + 57 + 58 + 59 + 60 71 + 72 + 73 + 74
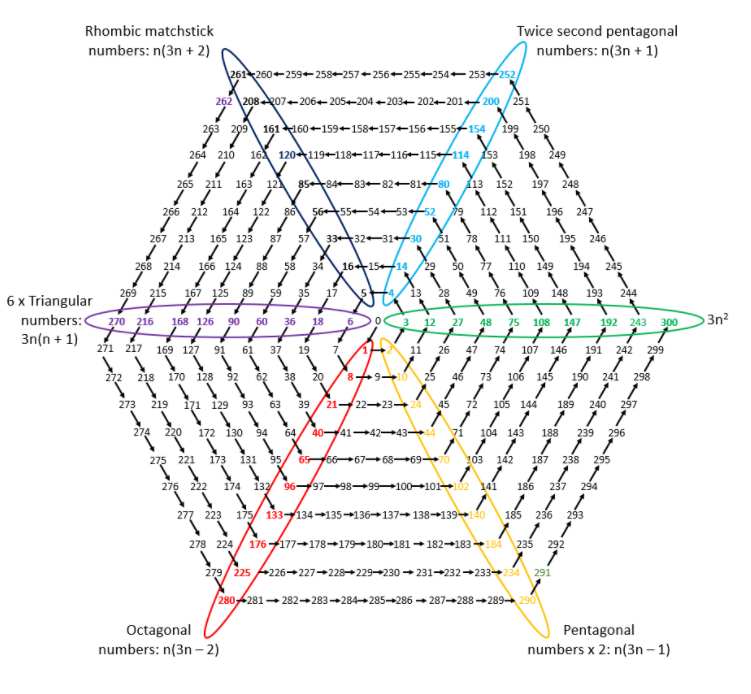
○ Cunningham numbers are those that can be expressed as one more or less than a perfect power; ○ 290 = 172 + 1
○ A sliding number is one that can be expressed as the sum of two numbers, the sum of whose reciprocals add up to the original number divided by some power of 10; ○ 290 = 40 + 250 and 1/40 + 1/250 = 0.0290 = 290/104; so 290 is a sliding number; ○ Sliding numbers are very rare—290 is only the 17th; the 600th sliding number is 2851006250, because it equals 409600000 + 2441406250 and 1/409600000 + 1/2441406250 = 0.000000002851006250 = 2851006250/1018.
○ Sphenic numbers are the products of three distinct primes; ○ 290 = 2 × 5 × 29; ○ 290 is therefore a sphenic number, and is thus the area of a cuboid with sides of length 2, 5, and 29 units.
290 is an untouchable number, one that cannot be expressed as the sum of all the proper divisors of any other number. For example, the proper divisors of 9 are 1 and 3, whose sum is 4; therefore 4 is a touchable number, since it is the sum of the proper divisors of 9. There is no integer whose proper divisors add up to 290.
Starting with zero, write the integers consecutively in a hexagonal spiral, as follows: ○ Each of the diagonals in this spiral is a specific series of numbers. For example, the numbers in the red diagonal constitute the series of octagonal numbers, an example of which I showed in Interesting integer 280 ○ Each of the members of the series in the orange diagonal is twice a pentagonal number, including 290:
|