Since SARS-CoV-2 started causing covid-19 many different treatments have been studied, with varying degrees of success, mostly none. An incomplete list of pharmacological interventions that have been registered in clinical trials is shown in Box 1.
Box 1. An incomplete list of compounds that have been included in clinical trials of the treatment of covid-19; many are intended to affect (enhance or inhibit) the immune system; some are intended for symptomatic relief; of those that are intended to inhibit replication of the virus, many are based on in vitro observations
So far these interventions, apart from dexamethasone, have either failed to produce benefit or at best have produced minor effects on relatively unimportant endpoints. Some may have caused harm.
How should we approach the problem pharmacologically? You can of course try any old drug, especially if it is an old drug, supposedly safe, simply because someone has reported an in vitro effect, but in that case don’t bet on success. There’s no guarantee that the in vitro milieu in any way resembles what goes on in vivo.
There are five general ways of approaching the problem (Box 2), and the higher up the list you can act the better. It is good to reduce mortality after infection, if you can. But preventing the infection in the first place has got to be the best strategy. Non-pharmacological measures may have done little, and finding a vaccine takes time. We can hope that vaccines, when we have them, will raise antibodies that are both long-lasting and of high affinity for the virus. There is, of course no guarantee that either of those desiderata will be fulfilled, but it is clearly an important strategy to pursue.
Box 2. Methods of preventing or treating covid-19; I omit methods for reducing spread of the infection after it has occurred, such as social distancing and masks, for which the published evidence either for or against is woefully poor

I know of no major pharmacological attempts to stop the virus binding to the ACE2 enzyme on the cell membrane or fusing with the membrane itself, but since the virus has at least two entry mechanisms via its glycoprotein spike, it is likely that at least two different compounds would be needed to achieve that directly. However, in both cases it is activation by a single serine protease, the TMPRSS2, acting on two separate sites on the spike, that allows it to gain access to the cell, so TMPRSS2 inhibitors might be indirectly effective. Two such inhibitors, nafamostat and camostat are currently in clinical trials.
Once the virus is inside the cell, there are various points of potential attack. Preventing it from being released from the endosomes that have carried it there didn’t seem an attractive strategy from the start, particularly in view of the adverse effects of the high doses of the drugs that were being proposed to do it, the 4-aminoquinolines chloroquine and hydroxychloroquine, if that’s how they work. And so it has proved so far. That the latter is still being trialled as pre-exposure prevention in healthcare workers may be, to paraphrase Dr Johnson, the triumph of hope over mechanistic reasoning, and difficult to assess.
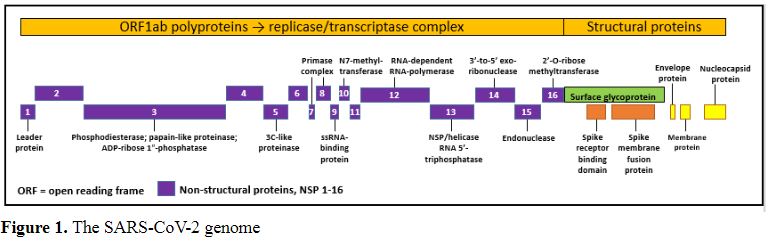
Once the virus has been released from the endosomes one can try to attack its structure in the hope of preventing replication. A schema of the viral genome is shown in Figure 1. The main point of attack that has so far been explored is its RNA-dependent RNA polymerase (nsp12), with drugs such as remdesivir and favipiravir. The results have been disappointing. The virus has repair mechanisms that may get in the way. Nor is it a surprise that drugs that were developed to affect mechanisms that the virus does not possess are ineffective. Lopinavir, for example, which inhibits an HIV protease, has been shown to have little or no efficacy.
As an almost last ditch, one can try modulating immune responses to the infection, enhancing them when it’s mild and suppressing them when it’s severe. Immune suppression with dexamethasone reduces mortality in severe infections, but it may increase mortality in mild cases, perhaps by impairing the beneficial immune responses. We still need to learn when and how to use it. The very last ditch is repairing or trying to mitigate the damage done.
There are very few acute virus infections that we are any good at treating once they’ve taken over. Some chronic virus infections are different; for example, multiple drug therapy is reasonably effective in HIV and hepatitis B. Perhaps we should use several drugs at once in covid-19. It’s like besieging an apparently impregnable castle. You’d attack it from all quarters. You might send your troops to tunnel under the back door; you’d send them round the sides to scale the walls; and you’d batter down the door at the front. Even if the Greek fire got some of them, there’s a chance that a few would get through. You’re more likely to succeed than by just attacking from one direction.
Jeffrey Aronson is a clinical pharmacologist, working in the Centre for Evidence Based Medicine in Oxford’s Nuffield Department of Primary Care Health Sciences. He is also president emeritus of the British Pharmacological Society.
Competing interests: None declared.
|
This week’s interesting integer: 282 Naming numbers All kinds of adjectival names are used to describe numbers, and I have mentioned some of them in previous entries in this series. The most familiar of these is “prime”. A prime number, of course, is one that is not divisible by any number other than 1 and itself. Prime numbers often figure (an appropriate word that) in the interest that an integer stimulates, even when the integer is not itself prime. 282 is, for example, an interprime number, since it is equidistant from 281 and 283, both primes. And 282 + P282 (the 282nd prime number) is also prime (282 + 1831 = 2113). In Giovanni Resta’s endlessly fascinating Numbers Aplenty website, upwards of 200 of these names are listed, from ABA numbers (any that can be expressed in the form A×BA) to Zumkeller numbers (see below), of which 282 is an example. The names given to numbers come from various sources, some are named after the mathematicians who first described them or are in some way associated with them (e.g. Duffinian numbers, Kaprekar numbers, and Zumkeller numbers (see below); some are reversals (e.g. emirps, bemirps, and emirpimes, iccanobiFs, and tcefreps); some are puns (e.g. evil and odious numbers); some are fanciful, alluding to some property of the number or the way that is derived (e.g. happy, lucky, polite); and some are geometrical (square, triangular, pentagonal, heptagonal). One type of number is named after a fictional character, Achilles numbers, which I shall describe when we get to 288, which is also an ABA number. Here are some others, relevant to 282:
Numbers for which some proper divisor exists, call it D, such that subtracting D from the sum of the other proper divisors of the number leaves the number itself. 282 is an admirable number, since its proper divisors are 1, 2, 3, 6, 47, 94, and 141, and 282 = 1 + 2 + 3 + 47 + 94 + 141 – 6. [The proper divisors of a number are all of its divisors, including 1 but excluding the number itself.]
Numbers whose digits differ by one; 282 is aesthetic in base 8 (432) and base 9 (343).
Numbers the mean of whose divisors is an integer; the divisors of 282 are 1, 2, 3, 6, 47, 94, 141, and 282, the sum of which is 576 and the mean 72.
Numbers that have an even number of ones in base 2; 282 = 100011010; those that have an odd number are called odious.
282 is self-evidently palindromic, but it is also palindromic when expressed in other bases—2112 in base 5 and 343 in base 9.
Numbers whose digits do not decrease, although they may not increase. 282 is not itself plaindromic, but it is when expressed in bases other than 10: 237 in base 11, 189 in base 13, 13c in base 15, and 11a in base 16.
Numbers whose digits do not increase, although they may not decrease; 282 is not itself nialpdromic, but it is when expressed in bases other than 10: 552 in base 7 and 432 in base 8.
Numbers that can be expressed as the sums of consecutive integers; 282 =
An abundant number is one whose proper divisors add up to more than the number itself. The sum of the proper divisors of 282 is 294. A primitive abundant number is one none of whose proper divisors is also abundant.
Numbers that are the product of three primes; 282 = 2 × 3 × 47; it is therefore equal to the volume of a cuboid with sides of those lengths.
Numbers, denoted by Uk, that are members of the Ulam sequence, named after Stanislaw Ulam. The first two integers in the sequence are defined as U1 = 1, U2 = 2. For larger numbers, Uk is the smallest integer that can be written in exactly one way as Ui + Uj, with i < j < k. 282 = 102 + 180, both of which are Ulam numbers; no other Ulam numbers sum to 282.
Numbers whose digits alternately rise and fall, like 282, which also undulates in base 9, 343
Numbers that use fewer digits than their factorization. 282 = 2 × 3 × 47, which uses four digits, whereas 282 uses only three.
Numbers whose divisors can be partitioned into two distinct sets with equal sum. The divisors of 282 are 1, 2, 3, 6, 47, 94, 141, and 282. These can be divided into two sets with equal sums:
282 = 6 + 10 + 15 + 21 + 28 + 36 + 45 + 55 + 66 I haven’t seen a specific name for such numbers; I call them percussive, because they involve a lot of triangles.
282 = 44 + 45 + 46 + 48 + 49 + 50 I call such numbers family numbers, because they are the sums of mostly sibling numbers, the name I give to numbers that share a divisor, like siblings share a parent. The divisors of the six non-primes here that appear in more than one of each are 2, 3, and 5; 49 is the only number in the set that is not a sibling of any of the others. |
