Here’s an extract from a recent newspaper report: “The key aim of social distancing is to get this figure below one, at which point the outbreak would begin to peter out.” The figure to which this report refers is the basic reproduction number (or reproductive ratio) of a virus, called R₀ (R nought or R zero). It is estimated using data fed into epidemiological models, statistical and mathematical.

I have previously discussed the IndoEuropean root MED, to measure and hence to ponder, judge, or prescribe, as a source of words about medicine and medicines. Its o-grade form, MOD, has given rise to another wide range of words, via many Latin words such as modus, a measured amount, and modulus, a unit adopted as a standard of measurement. English words derived from these include mood, mode, modal, and modicum, modus, modulus, module, and modiolus, moderate and immoderate, modest and immodest, modern and modify, commode, commodious, commodity, and accommodate, mould, and of course model.

A model was originally (15th century) a set of designs for a proposed structure, and by analogy something that accurately resembles or represents something else, especially on a small scale. Later (17th century) it came to mean a small-scale three-dimensional representation, such as a maquette. But the idea of a model as a mathematical construct, simplifying a concept in a way that allowed computation, didn’t emerge until the end of the 19th century. Here it is in a paper from 1894 (Figure 1). 

Nowadays we recognize all kinds of statistical and mathematical models. They may be in purely mathematical form, with equations that embody a set of assumptions about the way in which a set of data behaves, such as the extent to which a sample was randomly generated and the probability distribution of the data. Or they may be in the form of a structural model in which, for example, compartments representing certain segments of a population or aspects of physiological or pharmacological processes are linked by mathematical representations of what happens when there is transfer from one compartment to another.

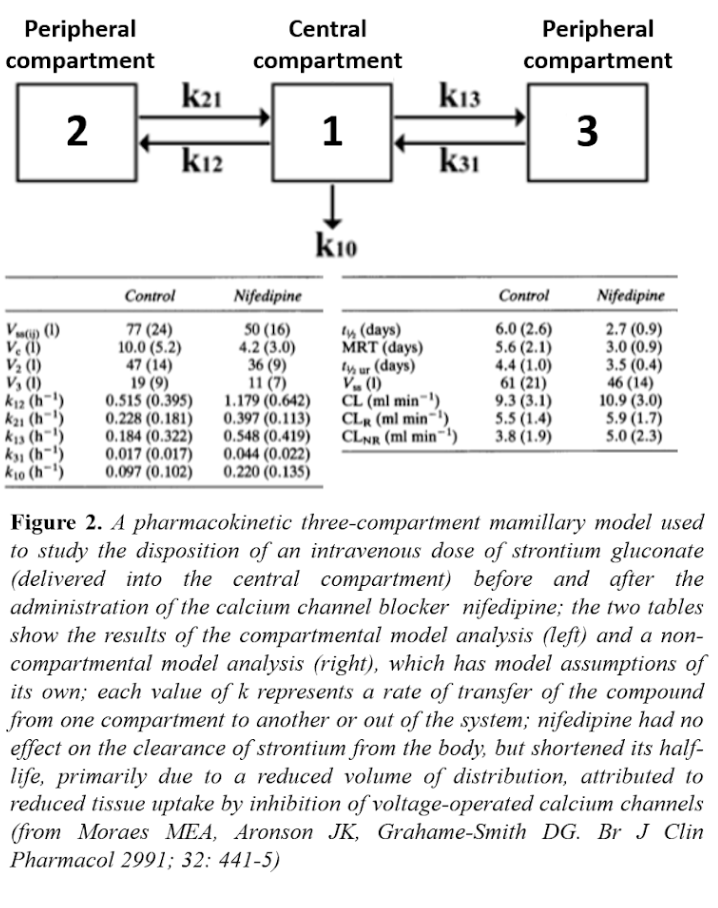
For example, in Markov models used in pharmacoeconomics the compartments typically represent disease states, between which individuals may move as their health state changes according to transition probabilities specific to each state and each period of time during which a change occurs (e.g. due to a therapeutic intervention). Figure 2 shows a pharmacological example—including both compartmental and non-compartmental analyses.

Formally a statistical model consists of the data set and a set of probability distributions supposedly associated with the set; in Bayesian models there is also an associated presumed prior distribution, which will be adjusted as more data accrue.

Such models can be used to estimate the basic reproduction number of a virus, R₀, defined as the number of cases that are expected to occur on average in a homogeneous population as a result of infection by a single individual, when the whole population is susceptible at the start of an epidemic, before immunity starts to develop and before any attempt has been made to immunize the population.

If one person develops the infection and passes it on to two others, the R₀ is 2. If the average R₀ in the population is greater than 1, the infection will spread. The higher the value of R₀, the faster an epidemic will progress, although R₀ does not specify how fast. If R₀ is less than 1, the infection will spread only slowly, and it will eventually die out.

R₀ is estimated from data collected in the field and entered into mathematical models. The estimated value depends on the model used and the data that inform it. A typical model is based on three factors: individual susceptibility to the infection, the rate at which infections actually occur, and the rate of removal of infection from the population, by either recovery or death. As immunity develops in the population the value of the reproduction number changes; it is then called the effective reproduction number (Re). When Re falls below 1 the infection will die out. That, as the newspaper report told us, is what we are currently waiting for.

Next week I shall discuss how well the models work.

Jeffrey Aronson is a clinical pharmacologist, working in the Centre for Evidence Based Medicine in Oxford’s Nuffield Department of Primary Care Health Sciences. He is also president emeritus of the British Pharmacological Society.

Competing interests: None declared.

This week’s interesting integer: 268 ● Like 262, 268 is an untouchable number, an integer that cannot be expressed as the sum of all the proper divisors of any other number. For example, the proper divisors of 9 are 1 and 3, whose sum is 4; therefore 4 is a touchable number, since it is the sum of the proper divisors of 9. There is no integer whose proper divisors add up to 268. Untouchable numbers are also called non-aliquot numbers. ● Prime connections: (a) Twin primes are consecutive primes (e.g. 41 and 43). 268 is related to twin primes in two different ways:      (i) the 268th prime is 1721 and the 269th is 1723       (ii) 6 × 268 + 1 = 1607 and 6 × 268 – 1 = 1609 (b) The 268th prime, 1721, minus 268 equals another prime, 1453 (c) And the average of the squares of all the prime factors of 268 (2, 2, and 67) is also prime: (22 + 22 + 672)/3 = 1499 (d) 268 is the sum of two consecutive primes (131 + 137) ● 268 is palindromic in base 8 (414) ● 268 is an even lucky number, so called because it survives the following sieving process: (a) List the even integers, starting with 2:    2 4 6 8 10 12 14 16 18 20 22 24 26 28 30 32 34 36 38 40 42 44 46 48 50 52 54 56 … (b) Remove every fourth number:   2 4 6 10 12 14 18 20 22 26 28 30 34 36 38 42 44 46 50 52 54 58 60 62 66 68 70 … (c) The first lucky number to survive is 6, so now remove every sixth number: 2 4 6 10 12 18 20 22 26 28 34 36 38 42 44 50 52 54 58 60 … (d) The next lucky number to survive is 10, so now remove every tenth number:    2 4 6 10 12 18 20 22 26 34 36 38 42 44 50 52 54 58 … (e) Now remove every twelfth number and so on; the list that emerges is as follows:     2 4 6 10 12 18 20 22 26 34 36 38 42 44 50 52 54 58 68, 70 76, 84, 90, 98, 100, 102, 108, 114,116, 118, 130, 132, 138, 140, 148, 159, 164, 170, 172, 178,182, 186, 196,  198, 212, 214, 218, 228, 230, 234, 244, 246, 260, 262, 268, … See also Interesting integer 261.