Hwæt!

Several Old English poems begin thus, followed immediately or soon after by some variant of “we have heard ….”. The best known example is that of Beowulf, which dates from between 1200 and 1300 years ago. Here are the first three lines, with my own translation in parallel text:

Hwæt wē Gār-Dena  in gear-dāgum         We have heard, no doubt, of the bygone glory 

þēod-cyninga  þrym gefrūnon                   of the kings who courageously ruled the Danes.

hu ðā aeþelingas  ellen fremedon            And those peerless princes’ heroic exploits.

Note the absence of an exclamation mark after the first word. As the manuscript of Beowulf held in the British Library (MS Cotton Vitellius A.xv) shows, the original contained no exclamation mark. Indeed it contained no punctuation marks at all. Jakob Grimm, in his Deutsche Grammatik (1837) introduced an exclamation mark after “Hwæt”, contending that it was purely an exclamation. But it has been suggested that it is no exclamation at all.

I first read Beowulf in 1959, in a prose translation by David Wright, first published in 1957 in Penguin Classics, and have since accumulated more editions. Most of them translate “Hwæt” as some form of exclamation (Figure 1). But in 2013 George Walkden argued, from an examination of instances of “hwæt” in Old English texts, that the word was not an interjection, but “an underspecified wh-pronoun introducing an exclamative clause” and “parallel to how”, as in “How you’ve changed”.

K^WO was the IndoEuropean root of a range of relative and interrogative pronouns, like the Latin quis, quis, quid, and adjectives, like qui, quae, quod. In Old Germanic words it became hw, whence it entered Old English. This spelling persisted until the late 13th century, but by the 12th century it was already beginning to be replaced by wh, perhaps affected by words that came from different IndoEuropean roots, such as whelk (from WEL, to turn or roll), whip (from WEIP to vacillate or tremble ecstatically), and whit (from WEKTI, a thing). Some 13th century spellings used qu, or in Scotland quh, as in the family name Colquhoun. Furthermore, dialectic variations in pronunciation led in some cases to omission of the aspirate (Figure 2).

The spelling of “hwæt” tells you how it was pronounced. First an aspirated |h|, then the voiced bilabial |w|. The digraph |æ|, called aesc, is pronounced like the flat a in ash.

The Chambers Dictionary (12th edition, 2011) includes about 150 headwords beginning with wh-; almost all are pronounced (h)w; for example: what (descended from “hwæt”), when, whither, whop, whup, and why. There are two groups of exceptions:

• the Maori loanwords whanau (an extended family), pronounced fä’now, whare (a house), pronounced fär’ā, and whenau (land), pronounced fen’oo-ə.
• most words beginning with a long o, including who, whodunnit, whom, and whose, whole and whore, all of which are pronounced with an initial h-.

Which brings me to whooping cough and a question that recently appeared on Twitter:

The sound that you hear in this condition was originally called a hoop, which is what it sounds like—a long intake of breath after a series of short violent coughs. The first instance listed in the Oxford English Dictionary dates from 1811, in Robert Hooper’s edition of Quincy’s Lexicon-medicum, under Pertussis: “The cough … is attended with a peculiar sound, which has been called a hoop.” “Hoop” in this sense antedates the use of “whoop” by about 200 years.

The OED first attests the two different spellings of the name of the disease in quotes from 1739 (“whooping cough”) and 1758 (“a hooping, or any nervous cough”). But I have found an antedating, from 1701 (Figure 3), which gives “hooping cough” precedence. 

So “whooping cough” is pronounced, like who, whose, and whom, with an initial h, just as it is given in the OED: /ˈhuːpɪŋkɒf/

But, given the history of “hwæt”, perhaps it is not surprising that the Twitter comment about this ended with the exclamation “What the what!??”.

Jeffrey Aronson is a clinical pharmacologist, working in the Centre for Evidence Based Medicine in Oxford’s Nuffield Department of Primary Care Health Sciences. He is also president emeritus of the British Pharmacological Society.

Competing interests: None declared.

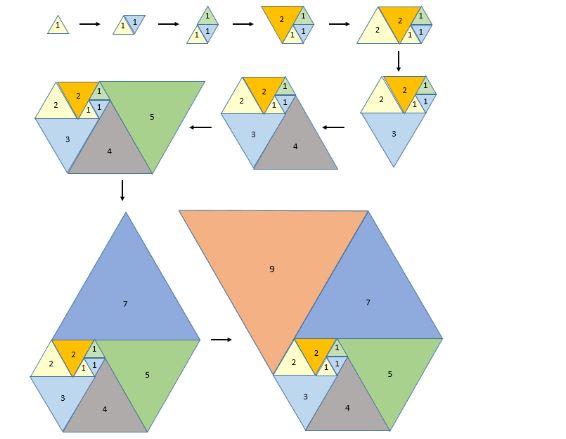
This week’s interesting integer: 265 • 265 is the sum of two consecutive squares and two non-consecutive squares: 265 = 112 + 122 = 121 + 144 = 32 + 162 = 9 + 256 • 265 is a member of the Padovan sequence, named after Richard Padovan, who presumably has an ancestor from Padua. The sequence is illustrated below. Starting at the top left corner we draw an equilateral triangle, side length 1 (yellow). We draw another unit triangle next to it (blue) and then another above that one (green). Now we keep adding triangles, always laying them along the longest available side: length 2 (orange), length 2 (yellow), length 3 (blue), length 4 (grey), length 5 (green), length 7 (blue), and length 9 (salmon). We can go on doing this ad infinitum, and the Padovan sequence is the side-lengths of the triangles in the order in which they are added: 1, 1, 1, 2, 2, 3, 4, 5, 7, 9, 12, 16, 21, 28, 37, 49, 65, 86, 114, 151, 200, 265 Each member, n, starting with the first 2 in the sequence, is formed from (n–2) + (n–3). So, 265 = 114 + 151 • 265 is the only three-digit subfactorial. Take the string of digits 1:2:3 Now create all the possible strings of these three digits in which none of them ever appears in its own original position. Here they are: 2:3:1 ⎯ 3:1:2 ⎯ just two of them pass the out-of-position test. Now try it with four digits 1:2:3:4. Here are all the possible arrangements: The ones in red pass the test. There are nine of them. !4 = 9 is the way this is written in mathematical symbols. If you have the time and the inclination you might want to try writing down all the permutations of 1:2:3:4:5:6. If you do, you will find that 265 of them pass the test. In other words !6 = 265. ! If you don’t want to bother, there is a formula that will do the work for you; here it is: !n = (n – 1)(!(n – 1) + !(n – 2)) • 265 is a Smith number, so called when Albert Wilansky noticed that the phone number (493-7775) of his brother-in-law Harold Smith had an interesting property: the sum of its digits is the same as the sum of the digits of its prime factors (3, 5, 5, and 65837): 4 + 9 + 3 + 7 + 7 + 7 + 5 = 3 + 5 + 5 + (6 + 5 + 8 + 3 + 7) = 42. So, 265 = 5 × 53 and 2 + 6 + 5 = 5 + 5 + 3 = 13 Smith numbers are also called joke numbers. Numbers of this type that do not have repeated prime factors are called hoax numbers. So 265 is the tenth Smith number and the twelfth hoax number. • 265 is a semi-Sophie Germain semiprime, i.e. a semiprime (the product of two primes) both of which are Sophie Germain primes, i.e. for which 2p + 1 is also prime. Thus. 265 = 5 × 53 both of which are Sophie-Germain primes, since 2 × 5 + 1 = 11 and 2 × 53 + 1 = 107. For more Sophie Germain primes see Interesting Integers 259, 262, and 263.