There is currently a discussion about the differences between related aspects of speech—dialect, accent, and diction.
Dialect is a form of a language that is peculiar to a specific region. The term is usually taken to mean any dialect other than the standard one, such as Standard English.
The IndoEuropean root LEG meant to gather or set in order, to consider or choose, and hence to read or speak. It gave the Greek words λόγος, word, speech, discourse, or reason, and λέγειν, to gather, recount, and speak. These give us the English words logarithm, logic, and logodaedaly; words ending in –ology and –logue (catalogue, decalogue, dialogue, epilogue); lexicon and words ending in –lexia (alexia, dyslexia); and words ending in –lect (analect, intellect, collect, and of course dialect). We get our word dialect from the Greek word διάλεκτος, discourse, debate, argument, conversation, speech, and language.
Linguistics experts have taken the –lect from dialect and coined several other words: acrolect, the most prestigious dialect of a language, basilect, the least prestigious, and mesolect, an intermediate variety, usually having features in common with both the acrolect and the basilect. A cryptolect is a secret language. An idiolect is a dialect peculiar to an individual, which may differ from the varieties of the same dialect used by others. And a sociolect is a dialect used by a particular social group or class. “Genderlect”, The Feminist Dictionary by Cheris Kramarae and Paula A Treichler tells us, is “a notion invented in the early 1970s to suggest overall characterizations of sex differences in speech.” It then says that “[this] portrayal now seems too abstract and overdrawn”, “now” being 1985. But the term is still being written about.
Dialect is typically marked by vocabulary. My Scottish dialect, for instance, includes words such as swithering (in a state of hesitancy or doubt) and dreich (dreary, usually as applied to the weather). It also includes English words used in senses other than are commonly used in England: to go the messages means to do the shopping, and the vegetable known as a swede in England is called a turnip in Scotland.
Dialect and accent usually go together. Scottish dialects, for instance, are typically spoken with a Scottish accent, because they both come from the same place. But the two are not indissolubly linked. And some people are bilingual, able to switch from dialect to Standard English at will.
The IndoEuropean root KAN meant to sing, giving the Latin verb cantare, to sing or to talk about something. This gives us chant and enchanting, cantata, cantor, incantation, descant, recant, and plain cant, the dialect of a class, originally beggars, but now pejoratively extended to any class. Add the Latin prefix ad to cantare and you get accantare, to sing to someone, from which comes accentus, intonation or accent. Accent originally (late 14th century) referred to the way in which something was sung, but it was later applied to the stresses in speech; marks placed above syllables to indicate such stresses were then called accents. Then in the late 16th century it came to mean the way of pronouncing a language.
Although stress, pitch, and rhythm are also involved, the way you pronounce your vowels is a primary characteristic of accent. For example, you can differentiate US and Canadian accents by listening to some of the vowel sounds, for instance in the word “out”; Canadians pronounce it somewhere between the US “owt” and the Scottish “oot”. Australian and New Zealand accents also have different vowel sounds, although the differences are hard to detect.
The foreign accent syndrome is a rare abnormality in which brain damage, typically frontal, or a psychogenic abnormality causes an individual to speak with a foreign accent. The most striking example I have seen was in a young English woman who started speaking with a beautiful French accent after an anaesthetic. Often, however, the accent is not clearly identifiable. We think of accent as something that is conditioned by listening to the people around us, particularly as we grow up. But cases of foreign accent syndrome, rare though they are, show that it’s a lot more complicated than that.
Jeffrey Aronson is a clinical pharmacologist, working in the Centre for Evidence Based Medicine in Oxford’s Nuffield Department of Primary Care Health Sciences. He is also president emeritus of the British Pharmacological Society.
Competing interests: none declared.
|
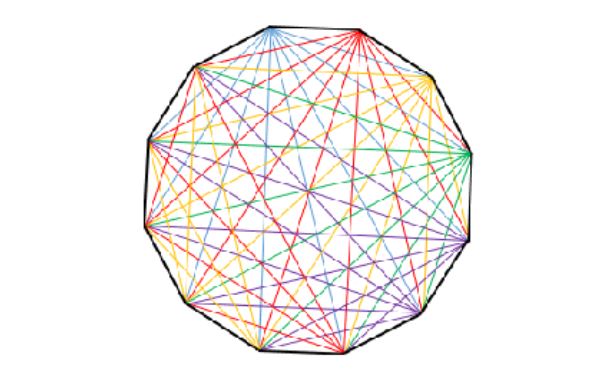
This week’s interesting integer: 341 Geometric numbers Dodecagonal intersections ● Join every pair of points in a dodecagon; there are 341 intersections:
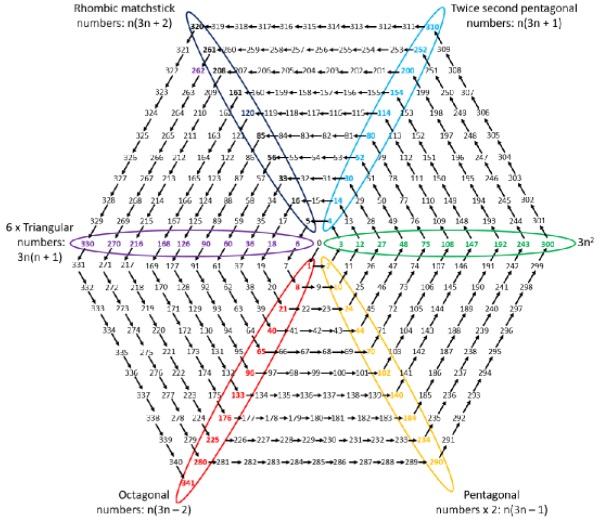
Octagonal numbers
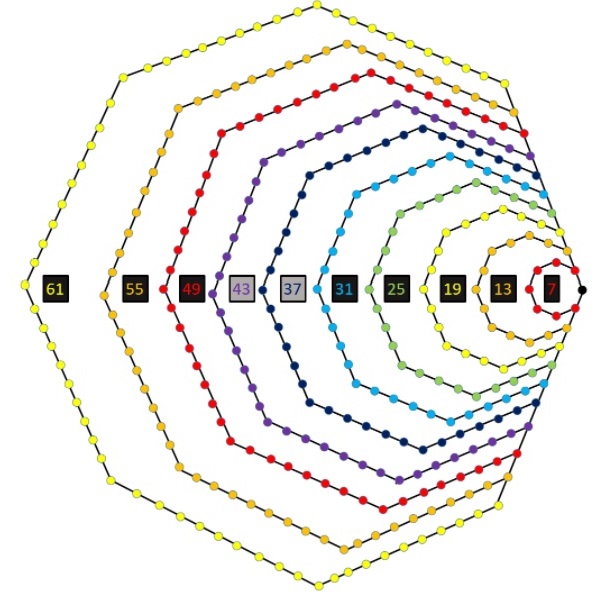
● The octagonal numbers also turn up in a hexagonal spiral (the red numbers in the picture below); 341 is in the bottom left-hand corner:
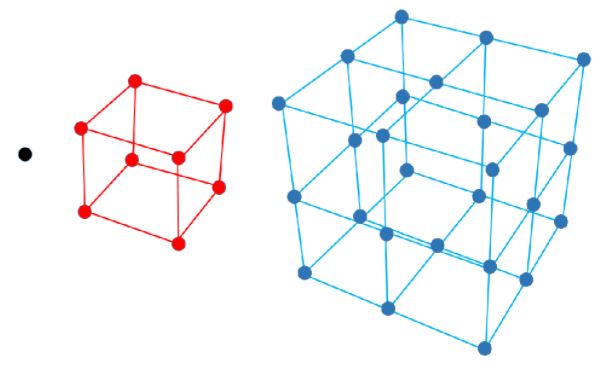
Centred cube numbers
Tiling rectangles
…….
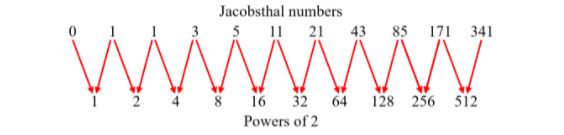
Jacobsthal numbers
1/2 – 1/4 = 1/4
Thus, the ratio of successive pairs of Jacobsthal numbers tends to 2 as the series tends to infinity. This property is not found in any other Fibonacci-type sequence in which the nth member (Mn) of the sequence is calculated as Mn = M(n–1) + k × M(n–2) Named numbers
Palindromes
Primes and semiprimes
Pythagorean
341 420 541 Sums of 341
170 + 171
170 + 171
Toothpicks
Miscellaneous
|