All hypotheses are unequal; some are more unequal than others.

I have previously discussed the Indo-European root DHE. The basic root, the so-called e-grade form, DHE, means to set or put down, to make or shape. But vowels change readily, by the mechanism that Jakob Grimm called ablaut (literally an off-sound). So there is also an o-grade form, DHO, and a zero-grade form, DHƏ, in which the final vowel is a neutral vowel sound called a schwa, after the Hebrew vowel of that name. The schwa, represented by an inverted e (lower-case ə or upper-case Ə) typically occurs in weakly stressed syllables, like the e in “hypothesis” (/hʌɪˈpɒθəsᵻs/). These various forms can also have prefixes and suffixes and may be reduplicated. This gives rise to a myriad of words, examples of which follow.

DHE gives deed, misdeed, and the obsolete alms-deed; as Queen Margaret says of Richard Duke of York in Henry VI, “Murder is thy alms-deed—Petitioners for blood thou ne’er putt’st back”. DHO gives us do, doing, and done. DHEM gives deem and theme, and DHOM gives doom and words ending -dom, like leechdom. Abdomen is conjecturally from the Latin abdere (ab + dare), to put away or conceal. DHEK gives theca (Greek θήκη), a sheath that encloses an organ, and apothecary, from the Greek ἀποτιθέναι to put away and hence ἀποθήκη a storehouse. And reduplication, DHE-DHƏ, gives the Greek verb τιθέναι, to put or place, which yields the trilogy of dialectical materialism, thesis, antithesis, and synthesis.

“Theory” is thought to come from two Greek words meaning to see, θεᾶσθαι and όράειν. However, I venture to suggest that it may have come from τιθέναι + όράειν, to place in view.

So a hypothesis, literally “placed underneath” (ὑπό), is a foundation, and hence the basis of an argument or a supposition. When it first entered English in the late 16th century it meant a particular case of a general proposition, and later the proposition itself. In logic it meant a supposition or condition forming the antecedent of a proposition. When Sir Thomas Browne used the word in his Pseudodoxia Epidemica in 1646, he meant, invoking the definition in the Oxford English Dictionary, “A provisional supposition from which to draw conclusions that shall be in accordance with known facts, and which serves as a starting-point for further investigation by which it may be proved or disproved and the true theory arrived at.”

This definition, unrevised since 1899, needs some attention. Hypotheses are indeed typically based on known facts and serve as starting points for further investigation, but only as such. It is easy to formulate explanations of phenomena once they have been observed, but wrong to accept them as gospel without further testing. However, to assert, as the OED’s definition does, that by such testing a hypothesis can thereby be proved is misleading. As Karl Popper taught us in The Logic of Scientific Discovery (1959), originally published in German in 1934 as Logik der Forschung, the proper way to test a scientific hypothesis is to try, not to prove it, but to disprove it, to falsify it, as Popper put it. Here is what he wrote: 

“A scientist constructs hypotheses, or systems of theories, and tests them against experience by observation and experiment.” Denying the validity of induction, he suggests that “inference to theories, from singular statements which are ‘verified by experience’ … is logically inadmissible.” He then goes on:

But today Popper’s principle is being abandoned. During the pandemic, researchers, presumably supported by the ethics committees that scrutinize their proposed studies, have decided that masked, randomized, placebo-controlled trials are not necessary in testing treatments for a serious infection, with few grounds for assuming that they will be efficacious, or, even if efficacious, that the balance of benefit and harm will be favourable.

In Greek ὑπόθεσις meant, among several things, a proposal or a proposed action, a suggestion or advice, an excuse or pretext, a practical problem or a supposition. Aristotle used it to mean the assumption of the existence of some scientific object. Today this meaning seems to be being espoused once more. Instead of testing their hypotheses, instead of trying to falsify them, researchers are trying to prove them. Next week I shall discuss how we should be grading therapeutic hypotheses and testing them in different ways.

Jeffrey Aronson is a clinical pharmacologist, working in the Centre for Evidence Based Medicine in Oxford’s Nuffield Department of Primary Care Health Sciences. He is also president emeritus of the British Pharmacological Society.

Competing interests: none declared.

 

This week’s interesting integer: 274   274 is a Tribonacci number. The series of Fibonacci numbers, first described by Leonardo of Pisa (Fibonacci) begins with 0, 1 and continues by adding the two previous numbers: 0, 1, 1, 2, 3, 5, 8, … The series of Tribonacci numbers starts with 0, 0, 1 and continues by adding the three previous numbers: 0, 0, 1, 1, 2, 4, 7, 13, 24, 44, 81, 149, 274, …   274 is a semiprime, i.e. the product of two primes, 2 × 137. It is also an interprime, the average of two consecutive primes, 271 and 277.The sum of its prime factors (2 + 137 = 139) is also prime.   274 is a Smith number, so called when Albert Wilansky noticed that the phone number (493-7775) of his brother-in-law Harold Smith had an interesting property: the sum of its digits is the same as the sum of the digits of its prime factors (3, 5, 5, and 65837) 274 = 2 × 137 and 2 + 7 + 4 = 2 + 1 + 3 + 7 = 13            Smith numbers are also called joke numbers. Numbers of this type that do not have repeated prime factors are also hoax numbers; 274 is the eleventh Smith number and the thirteenth hoax number.   274 is the sum of three non-zero squares in three ways:  274 = 32 + 32 + 162 = 32 + 112 + 122 = 72 + 92 + 122   274 is the sum of four squares, a2, b2, c2, and d2, such that a2+ b2, c2 + d2, a2 + d2, and b2 + c2 are all prime: 274 = 132 + 102 + 22 + 12 132 + 102 = 269; 22 + 12 = 5; 132 + 22 =173; 102 + 12 = 101   The square of 274 is the sum of 24 consecutive squares: 2742 = 442 + 452 + 462 + ……652 + 662 + 672   The proper divisors of a number are all the numbers that divide it apart from the number itself. 274 is the sum of the squares of 1, 2, 3, 4, 6, 8, and 12, which are the proper divisors of 24.   274 is a member of Moessner’s Magic Factorial Triangle. In 1951 the mathematician Alfred Moessner discovered a method for generating series of consecutive squares, cubes, fourth powers, and so on. The variant of his method shown here generates the series of factorial numbers n! ( i.e. 1, 1 × 2, 1 × 2 × 3, ….. 1 × 2 × 3 × …. × n). 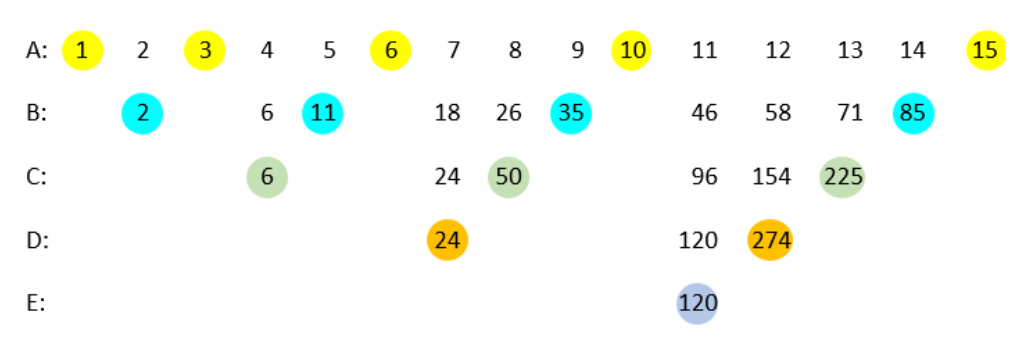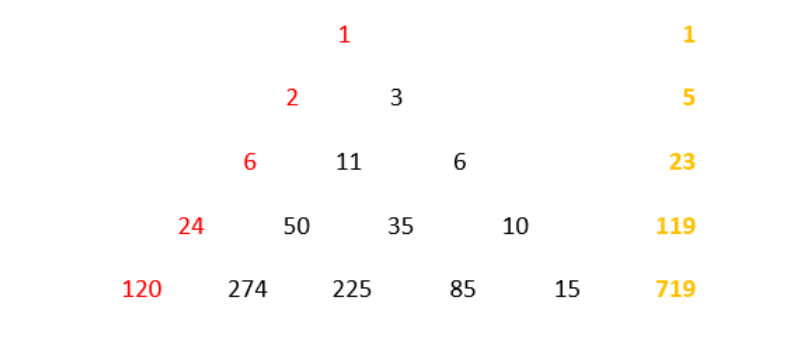Here’s the method:      A)  Write the counting numbers from 1 onwards in a row. Cover the triangular numbers (1, 1 + 2, 1 + 2 + 3, etc); these are coloured yellow in the diagram below.    B)  Add the numbers that are left uncovered in row A to make the partial sums shown in row B. Cover the numbers to the right of each section of numbers (coloured blue).    C)  Add the uncovered numbers as before and write the partial sums in row D. Cover the numbers to the right (green).    D)   Repeat (orange).    E)   Repeat (mauve). The numbers on the extreme left of each row are the factorials 1!, 2!, 3!, 4!, and 5! The process can be continued ad infinitum by writing more numbers to the right of row A and continuing the downward progression. The coloured numbers above can be rearranged in a triangle, as shown below; the red numbers are the factorials and the orange numbers are the sums of the numbers in the corresponding lines of the triangle, in each case one less than the factorial that starts the next line.   Moessner’s magical process is akin to that of logarithms—it turns powers into multiplications and multiplications into additions.