There is widespread misunderstanding about the meaning of the mathematical idea of “exponential”. Here are some synonyms listed on a website called WordHippo: aggressive, epidemic, ascending, augmented, expanding, growing, mounting, rampant, rapid change, rapid growth, spreading, wanton. In contrast the site gives just one antonym: “nonexponential”. But there is a better antonym for the term “exponential increase”. It is “exponential decrease”. As the financial adverts say, the value of an investment can go down as well as up. And exponential increases aren’t always huge.
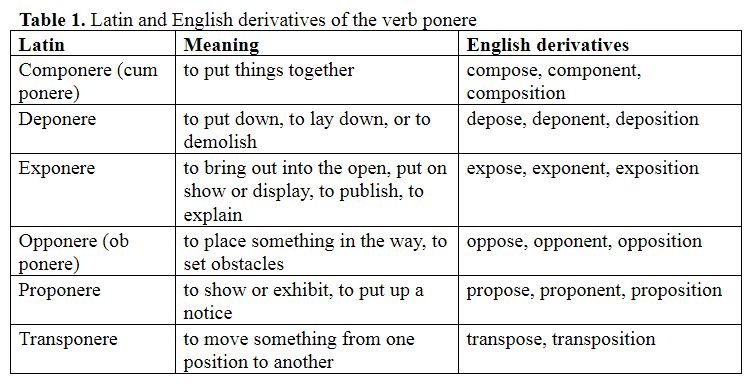
The Latin verb ponere meant to place or put in a specific position, to pitch camp, to lay the foundations of a building, to plant a tree, to put something aside, or to deposit money. Hence pose, posit, position, and positive. Table 1 shows the several Latin derivatives of ponere, formed by adding prefixes, and the English words we get from them.
Exponere meant to bring out into the open, put on show or display, to publish, to explain; hence expose, exposition, and exponent.
Exponere first made its mark on the English language in the 14th century, with the appearance of the now obsolete word “expone”, to set out in words or declare. In the 16th century “expone” was replaced in popularity by another 14th century word, “expound”, reflecting the French equivalent, expondre. Other words in the family went in a similar direction at about the same time: “compone”, to compose, was displaced by “compound”, and “propone”, to propose for consideration, gave way to “propound”.
“Exponent” entered the language in the 16th century at the same time as these changes were occurring, originally as an adjective, meaning interpretive, used to describe a logical proposition. It then became a noun, meaning one who sets something forth, expounds, or interprets. That didn’t happen until the early 19th century, but in the meantime mathematicians had adopted it to mean a symbol denoting the number of times a particular quantity is to be multiplied. For example in the number 23, the three is the exponent and it shows how many times you have to multiply 2 by itself to get the number so denoted: 23 = 2 × 2 × 2 = 8.
The story of exponential change begins with a man called John Napier, the eighth laird of Merchiston Castle near Edinburgh and the first exponent of logarithms. The castle was turned into a private boys’ school in 1833, but moved to new premises in the Colinton House Estate in 1930. Napier published his findings in 1614, in a book called Mirifici Logarithmorum Canonis Descriptio (A Description of the Wonderful Law of Logarithms).
In an arithmetical progression you start with a number and add another number to it, then repeat the process. An example is 2, 4, 6, 8, … in which you start with 2 and add 2 each time (these two numbers needn’t be the same). In a geometric progression you multiply instead of adding: 2, 4, 8, 16, … This progression can be rewritten using exponents: 21, 22, 23, 24, … and we can see that the exponents of the geometrical progression form an arithmetical progression. This suggests a method of multiplication: 23 × 24 = 23+4 = 27 (8 × 16 = 128). Or, more generally ab × ac = ab+c. It doesn’t matter what value we choose for a; we can conveniently use 10 instead of 2: 103 × 107 = 103+7 = 1010 (1000 × 10000000 = 10000000000; just count up the noughts).
Napier’s genius lay in recognizing that the exponent doesn’t have to be a whole number. For example, 100.3 × 100.7 = 100.3+0.7 = 101. In this case the exponent 0.3 is the logarithm of 2 and the exponent 0.7 is the logarithm of 5; and 2 × 5 = 101 whose exponent, 1, is the logarithm of 10. “Logarithm”, the word that Napier chose to describe his exponents, comes from the from the Greek λόγος a word, a proportion, or a ratio, and ἀριθμός, a number.
Logarithms convert multiplication into addition, and they convert the inverse process, division, into subtraction.
The next step is to realise that in the expression ab × ac = ab+c, not only do b and c not have to be whole numbers; neither does a. For example, 2.71833 × 2.71837 = 2.71833+7.
Next week I shall show why I chose to illustrate this using the number 2.7183 and explain why exponential increases aren’t always huge and how this idea of exponentiation tells us how a pandemic spreads.
Jeffrey Aronson is a clinical pharmacologist, working in the Centre for Evidence Based Medicine in Oxford’s Nuffield Department of Primary Care Health Sciences. He is also president emeritus of the British Pharmacological Society.
Competing interests: None declared.
