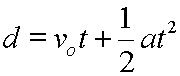This is it – a leap from the descriptive to the inferential. We are leaving the comfort of the sample we have collected data on and we’re about to make a statement that relates to the world beyond: we are inferring stuff.

Annoyingly, this first step is a phrase disturbingly close to another. The ‘standard error of the mean’ (aka ‘standard error’) is an number we can use to estimate how the mean of our sample relates to the mean of the population at large. In order to keep it clearly different in my mind than ‘standard deviation‘ I tend to think of it as ‘standard error of the mean’ and not  just ‘standard error’.

If we measure the height of all 25 children in Year 1 at one Yorkshire primary school, we’ll have an average height and we’ll have the spread of this data:

mean (x) = 103cm

standard deviation (σ) = 4cm

We can use this data to infer that the average height of all Year 1 kids in Yorkshire by calculating the standard error

standard error of the mean = standard deviation / square-root number of items (people) = σ / √n

standard error of the mean = 4 / √(25)

standard error of the mean = 4/5 = 0.8cm

… and estimating the 95% confidence interval using

limits = mean +/- 2*standard error of the mean

So the mean height in Yorkshire Year 1 primary children is 95% likely to be between 101.4cm and 104.6cm.

Using this approach will allow us to start making judgements about how the data we have may compare to other things, and if those comparisons are likely to be due to chance … in the next set of blogs.

In undertaking this estimate, we’re assuming that the primary school picked is representative of the population at large, that the measurements were accurate and that there was no systematic bias, for example either locking the smallest children in cupboards or making tall ones go into Year 2 classes. If any of these heinous offences have been committed then, quite apart from the investigations by police/GMC/Ofsted etc, we won’t be able to reaonsbly make inferences from the data. This is the same for real data too – which is why is is SO IMPORTANT to critically appraise the methods of the study for bias before tacking the ‘hard stuff’ in the numbers: as many folk have said, “you can’t polish a poo”.

– Archi