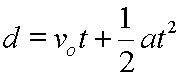You may well come across descriptions in the stats parts of papers that describe how the authors have derived their confidence intervals using an exact method.

Sounds very good, doesn’t it? Precise to the most precicestness.

And yet … sometimes an approximate confidence interval is better. You see, it all means what ‘exact’ exactly refers to …

The descriptions usually arise from a proportion; the number of patients with an outcome out of the total number of patients;

n / N

Now if the outcome happened to 10 patients, and there were 100 in the trial, this would lead to the proportion being:

10 / 100 = 0.1

The usual method of calculating CI is to find the standard error, and then go 1.96 up and down from the mean. When numbers get small (N=50 usually) this type of CI (called a Wald approximation) tends to be way too small, and runs into other problems, if the number of events (n) is tiny or nearly as big as N, so the proportion is ~0 or ~1, this approach leads to impossible confidence intervals, with negative proportions or proportions greater than 1. (And while we all know the boys gave 1.1 during the match ….)

An ‘exact’ confidence interval estimates what the ‘true’ proportion of patients with the outcome would be, if you had repeated trials, by assuming that the outcomes will follow a binomial distribution. Now this is much much better, but if the trial you are calculating the CI from is small (N small) then the CI is actually way too big.

What you’re actually wanting is not the ‘exact’ method, but something that approximates the truth a bit closer than either (the Wilson  or Agresti-Coull method). This gives relatively accurate 95% CI down to N=5

So despite the confidence imbued by the term ‘exact’, you actually want a (non-Wald) approximation for the CI of your proportions.

– Archi